Нормальні та дотичні напруження на похилих площадках

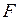Розглянемо стержень з поперечним перерізом , навантажений силою . У нормальному (перпендикулярному осі Z) перерізі виникають нормальні напруження , що визначаються як . А які напруження виникають на площадці , нахиленої до осі стержня під кутом ? Положення площадки визначається положенням її нормалі (рис.1.4а). Так як зовнішнє навантаження збігається з віссю стержня, то і на будь-якій похилій площадці внутрішні зусилля (повні напруження) збігаються з віссю стержня, у даному випадку повне напруження , що визначається як (рис.1.4б).

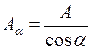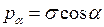Площа похилого перерізу , тоді . Але , а повне напруження . Так як , то завжди . Розкладемо повне напруження на дві складові: нормальну та дотичну до площадки (рис.1.4в). Одержимо нормальне 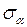і дотичне напруження на похилій площадці. Нормальне напруження на похилій площадці з нормаллю :

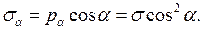(1.5)

Дотичне напруження на похилій площадці з нормаллю :

(1.6)

Нормальне напруження 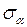позитивне (викликає деформацію розтягання), дотичне теж позитивне, тому що обертає розглянуту область щодо будь-якої точки у середині цієї області за годинниковою стрілкою. Визначимо напруження на взаємно перпендикулярній площадці , нахиленої до осі стержня під кутом b, що дорівнює (рис. 1.4г). Якщо , то, мабуть, і . Якщо підставити і з огляду на те, що , одержимо:

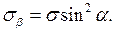(1.7)

Рис. 1.4. Напруження на похилих площадках

Аналогічно 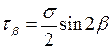. Підставивши , та з огляду на те, що , одержимо:

. (1.8)

Нормальне напруження також позитивне, а дотичне – негативне (обертає розглянуту область щодо будь-якої точки у середині цієї області проти годинникової стрілки). Склавши вирази (1.5) і (1.7), одержимо . Тобто, сума нормальних напружень на двох взаємно перпендикулярних площадках постійна. Порівнюючи (1.6) і (1.8), маємо 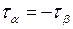. Ця рівність відбиває закон парності дотичних напружень: дотичні напруження на двох взаємно перпендикулярних площадках рівні по величині та протилежні по напрямку (знаку). Якщо відоме дотичне напруження t на одній площадці, то на інших площадках дотичні напруження визначаються за вищевказаним законом парності (рис. 1.4г). Аналізуючи вирази (1.5) та (1.7) слід зазначити, що максимальних значень нормальні напруження досягнуть в поперечних перерізах () та дорівнюють .

Дата добавления: 2015-07-20