Деформації та переміщення при розтяганні – стисканні. Закон Гука. Модуль пружності. Коефіцієнт Пуассона

Розглянемо розтягнутий силою 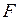стержень довжиною та площею поперечного перерізу (рис. 1.5).

Рис. 1.5. Деформований стан стержня

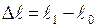Під дією зовнішнього навантаження, що розтягує, подовжній розмір стержня збільшується до . Зміна довжини називається абсолютним подовженням стержня.

Відношення

(1.9)

називається відносною подовжньою деформацією (чи просто подовжньою деформацією). Якщо в стержні виникає неоднорідний напружений стан, деформація в точці а визначається шляхом граничного переходу до нескінченно малого елемента довжиною :

(1.10)

Відносна подовжня деформація вважається додатною при розтяганні і від’ємною при стисканні.

При цьому необхідно зазначити, що в лінійних пружних системах існує прямопропорційна залежність між напруженнями та деформаціями.

(1.11)

Це співвідношення називається законом Гука при центральному розтяганні – стисканні (одновісному напруженому стані).

Коефіцієнт пропорційності – модуль пружності (подовжньої пружності) – фізична постійна матеріалу.

Орієнтовані величини модуля пружності для деяких матеріалів мають значення:

• сталь – =(2...2,1)×10⁵ МПа;
• мідь і сплави міді – =(1...1,2)×10⁵ МПа;
• алюміній і сплави алюмінію – =(0,7...0,72)×10⁵ МПа.

Враховуючи, що , , при центральному розтяганні – стисканні залежність між навантаженням та подовженням у межах пружних деформацій визначається співвідношенням , тут; – називається жорсткістю стержня при розтяганні.

Зміна довжини нескінченно малої ділянки стержня – , а зміна довжини всієї ділянки стержня (абсолютне подовження стержня довжиною ) визначається за формулою:

(1.12)

Крім подовжніх деформацій у стержні виникають і поперечні деформації. Різниця (рис. 1.5) називається абсолютною поперечною деформацією. Відношення називається відносною поперечною деформацією.

Відносна поперечна деформація в лінійно пружних системах має протилежний знак від відносної подовжньої деформації.

При цьому існує прямопропорційна залежність між відносною подовжньою та відносною поперечною деформаціями .

Абсолютна величина відношення відносної поперечної деформації до відносної подовжньої називається коефіцієнтом поперечної деформації чи коефіцієнтом Пуассона , тобто .

Значення коефіцієнта Пуассона для реальних матеріалів, що використовуються у машинобудуванні, розташовуються в діапазоні :

• для каучука близько до 0,5;
• для сталі – = 0,25...0,3;
• для міді – =0,31...0,35;
• для алюмінія – =0,32...0,36.

Коефіцієнт Пуассона також як і модуль подовжньої пружності є фізичною константою матеріалу та характеризує його пружні властивості.

Для ізотропних матеріалів і в усіх напрямках однакові (сталь, мідь, каучук, нешаруваті пластмаси), для анізотропних матеріалів і у різних напрямках різні (дерево здовж та поперек волокон, шаруваті пластмаси й ін.).

Якщо навантаження, що діє на стержень, є термосиловим, то в пружній області варто застосувати принцип суперпозиції деформацій, тобто:

(1.13)

де – пружна частина, а – температурна складова деформації, у якій – температурний коефіцієнт лінійного розширення.

Тоді

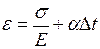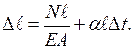, (1.14)

Слід відзначити, що у невеликих діапазонах температур і мало залежать від абсолютного значення температури.

Дата добавления: 2015-07-20