Потенційна енергія пружної деформації при розтяганні – стисканні

Потенційна енергія деформації, накопичена у пружному тілі, чисельно дорівнює роботі внутрішніх сил, виконаної в процесі деформування пружного тіла, тобто .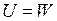

Розглянемо елемент стержня довжиною , навантажений статично (рис. 1.6а). У межах нескінченно малого елемента значення поздовжньої сили 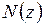у крайніх перерізах елемента з точністю до нескінченно малих першого порядка малості – однакові (рис. 1.6б). Елементарна робота зовнішніх сил чисельно дорівнює площі трикутника (рис. 1.6в), тобто .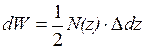

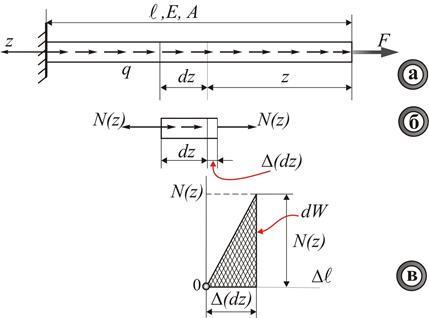
Рис. 1.6. Визначення потенційної енергії при розтяганні – стисканні

Але 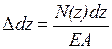, тоді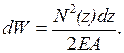

Повна робота є інтеграл по довжини стержня, тобто .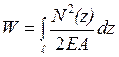

Враховуючи, що 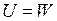, маємо:

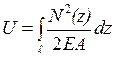. (1.15)

2 Статично невизначувані системи при розтяганні – стисканні

У практиці розрахунків при розтяганні – стисканні зустрічаються розрахункові схеми, для яких при відомих активних зовнішніх зусиллях, рівнянь статичної рівноваги недостатньо для визначення реактивних зусиль і внутрішніх зусиль. Такі системи прийнято називати статично невизначуваними.

Статично невизначуваною називається кінематично незмінна система, у якої число невідомих зусиль, включаючи реакції опор та внутрішні сили, більше числа рівнянь статики, які можна скласти для даної системи чи її частини.

Різниця між кількістю невідомих зусиль та кількістю незалежних рівнянь статичної рівноваги, що можна записати для всієї системи або її частини, називається ступенем статичної невизначеності системи.

Це число показує, скільки додаткових рівнянь у геометричному аналізі процесу деформування системи необхідно скласти, щоб можна було вирішити задачу. Розкриття статичної невизначуваності таких систем методом переміщень складається з чотирьох основних етапів.

Загальний план рішення таких задач полягає в наступному.

1. Статична сторона задачі (ССЗ). Визначаємо напрямок реакцій зв'язків, внутрішніх зусиль у стержнях, складаємо рівняння рівноваги, визначаємо ступінь статичної невизначуваності задачі.

2. Геометрична сторона задачі (ГСЗ). Установлюємо зв'язок між переміщеннями окремих перерізів конструкції, виходячи з умови спільності переміщень. Складаємо необхідну кількість рівнянь зв’язку між переміщеннями. Число таких рівність повинно дорівнювати ступеню статичної невизначуваності системи. Отримані рівняння називаються рівняннями спільності переміщень.

3. Фізична сторона задачі (ФСЗ). У рівняннях спільності переміщень для окремих елементів їхні переміщення виражаємо на підставі закону Гука через діючі в них невідомі зусилля.

4. Аналіз (синтез). Вирішуємо отриману систему рівнянь щодо невідомих зусиль.

Розглянемо розрахунки статично невизначуваних задач при центральному розтяганні – стисканні на прикладах.

Дата добавления: 2015-07-20