
Читайте также:
|
Стержньова система (рис. 2.2) складається з абсолютно твердого тіла  , шарнірно закріпленого у точці
, шарнірно закріпленого у точці  та підтримується стержнями 1 і 2 (довжини яких
та підтримується стержнями 1 і 2 (довжини яких 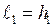 та
та 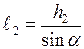 , площі поперечних перерізів
, площі поперечних перерізів 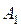 ,
,  , модулі пружності матеріалу
, модулі пружності матеріалу 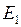 ,
,  ), система навантажена зовнішньою зосередженою силою
), система навантажена зовнішньою зосередженою силою 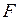 , власною вагою нехтуємо. Необхідно визначити внутрішні зусилля (виразити поздовжні сили в стержнях
, власною вагою нехтуємо. Необхідно визначити внутрішні зусилля (виразити поздовжні сили в стержнях  і
і  через зовнішнє навантаження
через зовнішнє навантаження 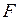 ).
).

Рис.2.2. Розрахункова схема до прикладу 4
1. ССЗ. Прикладаємо реакції опори 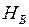 ,
,  ,
,  та
та  ..Застосовуємо метод перерізів до стержнів 1 та 2. При цьому внутрішні поздовжні сили
..Застосовуємо метод перерізів до стержнів 1 та 2. При цьому внутрішні поздовжні сили  і
і  , що виникають у стержнях дорівнюють реакціям опор
, що виникають у стержнях дорівнюють реакціям опор  та
та  .
.
Складаємо рівняння статичної рівноваги (для плоскої системи сил) через реактивні зусилля:
 (2.6)
(2.6)
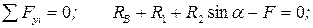 (2.7)
(2.7)
 . (2.8)
. (2.8)
2. ГСЗ. Під дією зовнішнього навантаження стержень 2 розтягається, стержень 1 стискається, а брус  займе нове положення
займе нове положення  (рис. 2.3). Відповідно точки
(рис. 2.3). Відповідно точки  и
и 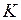 займуть положення
займуть положення 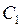 і
і  . Покажемо змінення довжин стержнів.
. Покажемо змінення довжин стержнів.

Рис.2.3. Деформована схема
Абсолютне значення укорочення стержня 1 –  .
.
Щоб знайти подовження похилого стержня 2, потрібно провести дугу довжиною 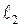 .
.
Через малість деформацій стержнів у порівнянні з розмірами стержневої системи переміщення точок С, D, K при повороті абсолютно твердого тіла вважаємо такими, що відбуваються не по дузі, а по дотичній до неї, по нормалі до первісного положення твердого тіла.
Подовження стержня 2 буде приблизно дорівнювати  , тобто
, тобто  .
.
З подоби трикутників  і
і  маємо:
маємо:
 .
.
З огляду на те, що  ,
,  ,
,  ,
,  , одержуємо:
, одержуємо:
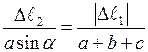 ,
,
або рівняння спільності переміщень одержуємо у вигляді:
 . (2.9)
. (2.9)
3. ФСЗ. З огляду на те, що зміна довжини стержнів визначається рівняннями:
 Þ
Þ  ,
,  , (2.10)
, (2.10)
то умова (2.9) прийме вигляд:  .
.
Після перетворень одержимо:
 . (2.11)
. (2.11)
4. Аналіз. Вирішуючи спільно рівняння (2.11) і (2.8), одержимо:
 (2.12)
(2.12)
Поздовжня сила  визначається з рівняння (2.11).
визначається з рівняння (2.11).
Відзначимо особливості стержньових статично невизначених систем. Переваги цих систем полягають у автоматичному перерозподілі зусиль між стержнями. До недоліків відноситься їх висока чутливість до неточності виготовлення та зміни температури.
Дата добавления: 2015-07-20; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Приклад 2. Жорстко закріплений стержень під дією температурного навантаження | | | Приклад 5. Монтажні напруження в стержньовій системі |