Читайте также:
|
1. Сила, действующая со стороны жидкости, всегда перпендикулярна к площадке, на которую она действует. Сила, отнесенная к единице площади поверхности, называется давлением
.
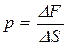Если сила, действующая на площадку, распределена по ней неравномерно, то
.
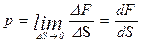1. Величина давления в данной точке жидкости характеризует степень сжатия жидкости и одинакова для всех направлений площадки, к которой отнесено давление.
2. Гидростатическое давление столба однородной жидкости на глубине h
.
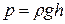3. Давление на двух различных горизонтальных уровнях отличается на величину, численно равную весу вертикального столба жидкости, заключенного между этими уровнями, с площадью сечения, равной единице,
,
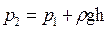где h – расстояние по вертикали между этими уровнями.
Закон Архимеда. На всякое тело, погруженное в жидкость или газ, действует со стороны этой жидкости (газа) выталкивающая сила, равная весу жидкости, вытесненной телом
,
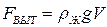где ρж – плотность жидкости; V – объем жидкости, вытесненной телом.
4. Стационарное течение идеальной жидкости.
а) Стационарным течением жидкости (или газа) называется течение, при котором все величины, характеризующие движение (скорость, давление, температура и т.д.), не изменяется со временем. При стационарном течении масса жидкости (или газа), проходящая за единицу времени через любое поперечное сечение трубки тока, одинакова для всех сечений
.
б) Уравнение неразрывности струи для несжимаемой жидкости (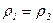
)
.
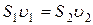т.е. скорость в любом сечении трубки обратно пропорциональна площади поперечного сечения.
в) Уравнение Бернулли для стационарного течения невязкой и несжимаемой жидкости для всех сечений данной трубки тока
,
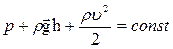где p – статическое давление в данном сечении; h – высота центра тяжести данного сечения над выбранным горизонтальным уровнем; ρgh – гидростатическое давление,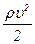 
– динамическое давление.
Для двух сечений уравнение Бернулли имеет вид:
.
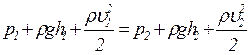Следствия из закона Бернулли:
если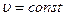 
,
;
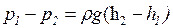если h 1 = h 2 (трубка тока горизонтальна),
.
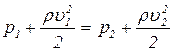5. Течение вязкой жидкости. Характер течения вязкой жидкости (газа) определяется безразмерной величиной, которая носит название числа Рейнольдса:
Re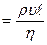 
,
где ρ – плотность жидкости; η – коэффициент внутреннего трения; 
и 
–характерные для данного потока скорость и линейный размер.
Для круглой трубы, а также для тела, имеющего форму шара, число Рейнольдса определяется по формуле:
Re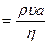 
,
где d – диаметр трубы или шара; – средняя по сечению трубы скорость течения жидкости (или скорость шара).
Для любого вида течения жидкости существует такое критическое число Рейнольдса, что при Re< Re кр возможно только ламинарное течение. Значение критического числа Рейнольдса зависит от ряда факторов: шероховатости стенок трубы, способа ввода жидкости в трубу и т. д.
Для гладких круглых труб
Re кр=2300.
Для шара, движущегося в вязкой среде,
Re кр= 0,5.
2 Ламинарное течение вязкой жидкости.
а) Сила внутреннего трения
,
где η – коэффициент внутреннего трения (или динамический коэффициент вязкости жидкости);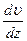 
– градиент скорости; ∆S – площадь поверхности соприкасающихся слоев.
б) Закон Стокса. Сила сопротивления, испытываемая шаром при его медленном поступательном движении в неограниченной вязкой жидкости, равна:
,
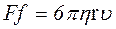где η – коэффициент вязкости; r – радиус шара; – скорость шара.
Закон Стокса справедлив при малых числах Рейнольдса (Re<Re кр).
Контрольные вопросы
1. Что называется давлением в жидкости или газе?
2. Давление – скалярная или векторная величина?
3. Зависит ли давление от ориентации площадки, к которой оно отнесено?
4. Что называется статическим и динамическим давлением?
5. В каких единицах измеряется давление в системе СИ? Выведите
соотношения между следующими единицами давления: 1 мм рт. ст., 1 атм.
6. Сформулируйте закон Архимеда. Где находится точка приложения
выталкивающей силы?
7. Какое движение называется стационарным?
8. Какие линии называются линиями тока? Что такое трубка тока?
9. Какая жидкость называется идеальной?
10. Сформулируйте теорему о неразрывности струи.
11. Сформулируйте закон Бернулли.
12. Следствием каких законов динамики является уравнение Бернулли?
13. При каких ограничениях был получен закон Бернулли?
14. Можно ли применить закон Бернулли к реальным жидкостям или газам?
15. Какие следствия вытекают из закона Бернулли?
16. Как определить скорость истечения жидкости из небольшого отверстия в
широком открытом сосуде?
17. Какое течение жидкости называется ламинарным?
18. Что характеризует число Рейнольдса? Определить число Рейнольдса для
цилиндрических труб, для тел, имеющих форму шара.
21. Что называется коэффициентом внутреннего трения? Его физический смысл.
Размерность коэффициента в системе СИ и СГС.
Дата добавления: 2015-07-20; просмотров: 83 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Динамика системы материальных точек | | | Силы трения |