Колебания

1. Гармонические колебания.

а) Гармонические колебания в системе возможны только при действии квазиупругой силы, т.е. силы, пропорциональной смещению и направленной к положению равновесия.

Динамическое уравнение движения

,

где k – коэффициент жесткости (сила, соответствующая смещению, равному единице).

Представим дифференциальное уравнение гармонического колебания в виде

,

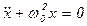где .

,

где x – смещение от положения равновесия; A – амплитуда колебания; φ₀ – начальная фаза.

б) Амплитуда и начальная фаза гармонических колебаний определяются из начальных условий. Если при , , то

, .

в) Период гармонического колебания определяется полностью параметрами системы и не зависит от начальных условий

.

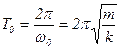г) Кинетическая энергия колеблющейся точки

.

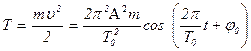Потенциальная энергия

.

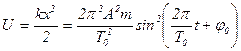При гармонических колебаниях справедлив закон сохранения механической энергии, ибо квазиупругая сила является консервативной

.

2. Затухающие колебания.

а) Если, кроме квазиупругой силы, действует сила сопротивления, то колебания будут затухающими. При малых скоростях сила сопротивления пропорциональна скорости движения. В этом случае динамическое уравнение движения записывается так:

, (1)

где r – коэффициент сопротивления.

Представим дифференциальное уравнение затухающего колебания в виде:

,

где – коэффициент затухания.

Решение этого уравнения:

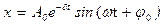, (2)

где A₀ – амплитуда в момент времени t=0, 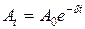– амплитуда в момент времени t; φ ₀ – начальная фаза колебаний; – циклическая частота затухающих колебаний.

Уравнение (2) имеет физический смысл при действительных значениях ω, т.е. при .

Если (случай большого трения), то решением дифференциального уравнения (1) является убывающая без колебаний функция x (t). В этом случае движение системы апериодическое.

б) Для характеристики затухания вводят, кроме коэффициента затухания , величину 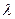, называемую логарифмическим декрементом затухания. По определению

.

Логарифмический декремент затухания связан с коэффициентом затухания формулой

.

3. Вынужденные колебания. Если, кроме квазиупругой силы и силы сопротивления среды, действует внешняя периодическая сила

,

то колебания будут вынужденными. Динамическое уравнение движения:

,

где F₀ – амплитуда вынуждающей силы; - циклическая частота вынуждающей силы. После процесса установления колебаний в системе возникнут вынужденные колебания, происходящие по закону:

.

Вынужденные колебания происходят с частотой вынуждающей силы. Амплитуда вынужденных колебаний

.

Сдвиг фаз φ между смещением и вынуждающей силой определяется следующим образом:

.

Амплитуда вынужденных колебаний и сдвиг фаз не зависят от начальных условий, а определяются свойствами системы, амплитудой и частотой вынуждающей силы.

При некоторой определенной частоте вынуждающей силы амплитуда достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной:

,

.

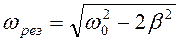Контрольные вопросы

1. Какие колебания называются гармоническими?

2. Что такое квазиупругая сила? Приведите примеры.

3. Запишите дифференциальное уравнение гармонических колебаний.

4. По какому закону изменяется смещение точки при гармонических

колебаниях? Дайте определение амплитуды, периода циклической частоты и

фазы колебания.

5. Выразите скорость и ускорение гармонически колеблющейся точки как

функции времени.

6. Получите формулы для кинетической, потенциальной и полной энергии при гармонических колебаниях.

7. Выведите формулы для периодов колебаний пружинного, математического и физического маятников.

8. Запишите дифференциальное уравнение затухающих колебаний и решение этого уравнения.

9. По какому закону изменяется амплитуда затухающих колебаний?

10. Что называется коэффициентом затухания, логарифмическим декрементом затухания? Каков физический смысл этих характеристик?

Дата добавления: 2015-07-20