Размещения без повторений.

Рассмотрим множество А = {a₁, a₂,...a_n }.Будем далее рассматривать размещения длины m элементов из множества А, не содержащие повторяющихся элементов, т.е. будем рассматривать такие соединения, которые отличаются друг от друга либо хотя бы одним элементом, либо порядком их расположения. При этом они не содержат повторяющихся элементов. Такие соединения называются размещениями без повторений и обозначаются .

При составлении таких соединений на первое место можно поставить любой из n элементов множества А, на второе – любой из n – 1 оставшихся элементов и, наконец. на m -е место – любой из n – (m – 1) оставшихся элементов. По правилу прямого произведения получаем, что общее число размещений без повторений из n по m равно = n(n – 1)(n – 2)...(n – m + 1) или

(*)

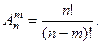П р и м е р 2. В хоккейном турнире участвуют 17 команд. Разыгрываются золотые, серебряные и бронзовые медали. Сколькими способами могут быть распределены медали?

Р е ш е н и е. 17 команд претендуют на три призовых места. Тогда указать команды, получившие золотую, серебряную и бронзовую медали, можно A ₁₇³ = 17∙16∙15 = 4080 способами.

Дата добавления: 2015-07-20