|
Читайте также: |
Если по оси абсцисс отложить 1/Т, а по оси ординат ln ơi, то получится прямая, отсекающая на оси ординат отрезок, равный ln ơ0 {рис. 7.8, а). Угловой коэффициент этой прямой равен — Egl2k, Строя такой график, можно определить постоянную ơ0 и ширину запрещенной зоны Eg.
Таким образом, у металлов концентрация носителей заряда практически не зависит от температуры, и температурная зависимость проводимости определяется температурной зависимостью подвижности; в полупроводниках концентрация резко зависит от температуры и температурная зависимость проводимости практически полностью определяется температурной зависимостью концентрации.
Примесная проводимость полупроводников. Температурная зависимость электропроводности примесных полупроводников определяется в основном температурой зависимостью концентрации носителей. На рис. 7.9, а схематически показаны кривые зависимости ơ (Т) для примесного полупроводника, содержащего различные количества активной примеси.
Рис. 7.9. Зависимость электропроводности примесных полупроводников от температуры: а — теоретические кривые; б —кривые для кремния, содержащего различные концентрации атомов фосфора
На этих кривых можно выделить три характерные области: первая соответствует низким температурам – до температуры истощения примеси Ts. Концентрация носителей заряда в этой области описывается формулой
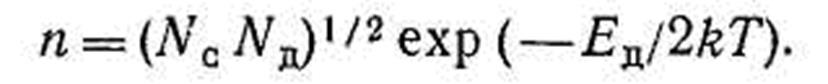(6.15)
Дата добавления: 2015-07-25; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| СОБСТВЕННАЯ И ПРИМЕСНАЯ ПРОВОДИМОСТИ ПОЛУПРОВОДНИКОВ | | | Где ơп0 — коэффициент, слабо зависящий от температуры. Логарифмируя , находим |