Прогнозная математическая модель динамики замещения

К числу вопросов, результаты исследования которых отражают тенденции развития техники, непосредственно относится прогнозирование скорости, с которой новые образцы техники будут вытеснять предшествующие образцы данного типа. Решение такой задачи представляет собой определение динамики замещения.

В данном случае объектом прогнозирования служит процесс внедрения новой техники, который может описываться изменением в течение времени отношения числа новых образцов (комплексов), в которых применяется новая техника, к суммарному числу образцов (комплексов), где они могут использоваться.

Пусть – некоторая мера распространения новой техники в момент времени (объем распространения);

– верхняя граница объема распространения новой техники на момент времени , выраженная в тех же единицах, что и .

При этом процесс замещения нового оборудования в некоторый момент времени значения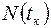

;

при ;

, при

.

Переменную можно назвать кумулятивной, или интегральной, функцией внедрения новой техники, значение которой в начальный момент времени зависит от того, что считать за начало внедрения: начало выпуска первых образцов новой техники или начальное поступление этих систем. В первом случае , в другом . Наиболее естественно первое предположение, хотя в ряде моделей может оказаться необходимым второе допущение.

В общем случае границы области распространения новой техники изменяются с течением времени, причем это изменение не имеет прямого отношения к процессу внедрения как таковому: сфера внедрения изменяется в соответствии с изменением взглядов на применение данного вида техники (задача о долевом участии). Можно считать, что в начальный момент времени значение заметно выше нуля. Изменчивость во времени границ области внедрения может исказить характер собственно процесса замещения, поэтому в ряде случаев вполне вероятно считать эту величину неизменной.

Введем новую переменную, которая обозначает относительное внедрение новой техники в момент времени :

.

При динамические характеристики совпадают с аналогичными характеристиками . Можно считать, что относительная интегральная функция внедрения – монотонно возрастающая функция времени, изменяющаяся в интервале [0, 1]:

;

.

Без существенных искажений реального процесса внедрения можно считать функцию непрерывной и дифференцируемой. Тогда дифференциальная функция внедрения

и дифференциальная относительная функция внедрения

всюду положительные, причем, как правило, к концу периода внедрения их значение монотонно убывает:

при .

Поскольку процесс внедрения имеет верхний предел и есть процесс насыщения потребностей, то целесообразно ввести еще одну переменную, характеризующую скорость приближения процесса к концу – интенсивность внедрения. Эта переменная определяет темп приближения процесса распространения нового к уровню полного насыщения в нем. Она определяется следующим образом:

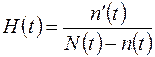
или

.

Функция насыщения или играет в моделировании динамики замещения центральную роль, так как она определяет конкретный вид функции или .

Несколько изменив последнее выражение, получим

.

Проинтегрировав это уравнение при ранее введенных допущениях, получим

при

и

при , так как .

Интенсивность замещения (функция насыщения) в общем случае может зависеть от самых различных экономических факторов, включая факторы, связанные с уровнем эффективности новой техники и относительным объемом капиталовложений на ее внедрение.

Поэтому функцию можно записать в следующем виде:

,

где – множество экзогенных факторов, определяющих конкретный процесс замещения.

Дальнейший анализ динамики процесса замещения состоит в спецификации вида функции , которую можно проводить исходя из эмпирических зависимостей и теоретических содержательных соображений.

Идентификацию этой функции можно провести, учитывая ее линейное приближение относительно :

,

где – уровень насыщения при ,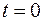

– скорость роста функции.

Здесь предполагается, что и не зависят от t, но могут зависеть от экзогенных переменных .

Интегрирование дифференциального уравнения

дает следующую интегральную функцию замещения при :

. (6.11)

Приняв или , можно получить два еще более простых варианта модели, которые чаще всего используются для описания динамики замещения.

При имеем

,

, (6.12)

где , то есть получаем для интегральной функции логистическую кривую. В данном случае в начальный момент времени , что вполне объяснимо с содержательной точки зрения.

При выражение (6.11) будет иметь вид

, (6.13)

то есть процесс замещения следует функции экспоненциального распределения вероятностей.

Из соотношений (6.11) – (6.13) можно получить также аналитические выражения и как функции времени.

Например, для имеем

при ;

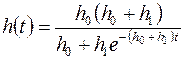при ;

при .

Графически функции (6.11) – (6.13) имеют вид s -образных кривых, что вполне согласуется с подавляющим большинством наблюдаемых данных. При этом интегральные функции замещения имеют точки перегиба 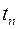, в которых скорость внедрения новой техники имеет максимальное значение.

Для функции (6.11) имеем

; ,

для логистической кривой (6.12)

; ; ; .

s -образный вид кривых позволяет аппроксимировать массив данных, характеризующий реальный процесс распространения новой техники во времени с помощью различных известных функций распределения вероятностей.

t, год m (t),%

Рис. 6.2. Динамика замещения

Так, например, обобщив функцию насыщения в выражении (6.13) в виде

,

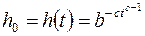получим интегральную функцию насыщения в виде распределения Вейбулла:

,

которое имеет также точку перегиба

.

Можно использовать и другие вероятностные распределения или иные аналитические зависимости, выражающие процессы с насыщением, имеющие горизонтальные асимптоты. Выбор модели можно осуществить с помощью регрессионного анализа и на основе содержательных соображений.

В качестве иллюстрации анализа динамики замещения используем относительное количество поступающих на рынок новых образцов оружия военной техники (обозначенное на рис. 6.2 ступенчатой линией) на период с 1980 по 2000 г. (всего рассматривалось 156 новых образцов). В данном случае процесс замещения с достаточной точностью аппроксимируется s -образной функцией вида

.

После определения параметров модели получаем зависимость

,

позволяющую (рис. 6.2) прогнозировать динамику замещения, высокая сходимость s -образной кривой с фактическими результатами свидетельствует о том, что предлагаемая модель пригодна для практического использования.

Дата добавления: 2015-07-25