
|
Читайте также: |
| Вопрос | Ответы | |
1. Среди функций:
1) 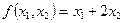 ; 2) ; 2) 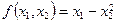 ;
3) ;
3) 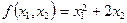 ; 4) ; 4)  ;
5) ;
5) 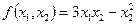 квадратичной формой является:
квадратичной формой является:
| 1) 1; 2) 2; 3) 3; 4) 4; 5)* 5 | |
2. Векторы 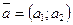 и и 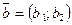 образуют базис в образуют базис в 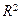 тогда и только тогда, когда определитель тогда и только тогда, когда определитель 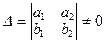 . Для проверки, образуют ли векторы . Для проверки, образуют ли векторы  и и 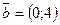 базис в базис в 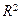 , необходимо составить определитель. , необходимо составить определитель.
| 1) 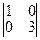 ; 2) ; 2) 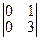 ; 3) ; 3) 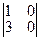 ; 4)* ; 4)* 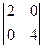 ; 5) ; 5) 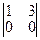
| |
3. Разложение вектора 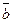 по векторам по векторам  , , 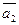 с коэффициентами с коэффициентами 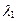 , ,  соответственно имеет вид: соответственно имеет вид:
| 1)* 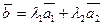 ;2) ;2) 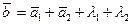 ;
3) ;
3) 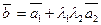 ; 4) ; 4) 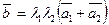 ; 5) ; 5) 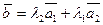
| |
4. Середина отрезка с концами 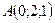 и и 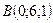 находится в точке: находится в точке:
| 1)  ; 2)* ; 2)*  ; 3) ; 3) 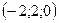 ; 4) ; 4) 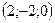 ; 5) ; 5) 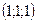
| |
5. Плоскость 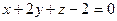 проходит через точку: проходит через точку:
| 1) 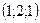 ; 2) ; 2)  ; 3) ; 3) 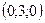 ; 4) ; 4) 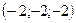 ; 5)* ; 5)* 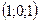
| |
6. Нормальным вектором плоскости 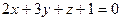 является вектор с координатами: является вектор с координатами:
| 1) 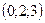 ; 2) ; 2) 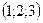 ; 3)* ; 3)* 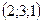 ; 4) ; 4) 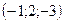 ; 5) ; 5) 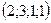
| |
7. Среди уравнений:
1) 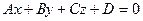 ;
2) ;
2) 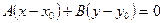 ;
3) ;
3) 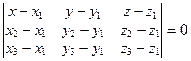 ;
4) ;
4) 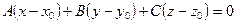 ;
5) ;
5) 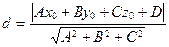 выбрать уравнение плоскости, проходящей через точку
выбрать уравнение плоскости, проходящей через точку 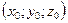 перпендикулярно вектору перпендикулярно вектору 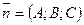 . .
| 1) 5; 2)* 4; 3) 3; 4) 2; 5) 1 | |
8. Направляющим вектором прямой 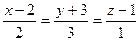 является вектор с координатами: является вектор с координатами:
| 1) 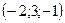 ; 2) ; 2) 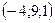 ; 3 ; 3 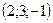 ; 4)* ; 4)* 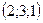 ; 5) ; 5) 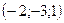
| |
9. Среди уравнений:
1) 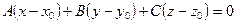 ;
2) ;
2) 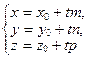 3) 3) 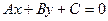 ;
4) ;
4)  ; 5) ; 5) 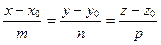 выбрать канонические уравнения прямой в пространстве
выбрать канонические уравнения прямой в пространстве 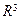 . .
| 1)* 5; 2) 4; 3) 3; 4) 2; 5) 1 | |
10. Решением системы линейных уравнений 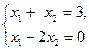 является упорядоченная совокупность действительных чисел: является упорядоченная совокупность действительных чисел:
| 1) 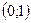 ; 2) ; 2)  ; 3)* ; 3)* 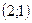 ; 4) ; 4) 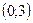 ; 5) ; 5) 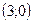
| |
11. Косинус угла 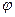 между прямыми между прямыми 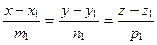 и и  находится по формуле находится по формуле 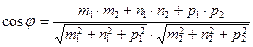 . Для нахождение косинуса угла . Для нахождение косинуса угла 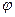 между прямыми между прямыми 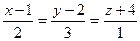 и и  необходимо найти значение выражения: необходимо найти значение выражения:
| 1) 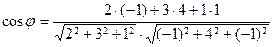 ;
2)* ;
2)* 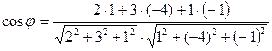 ;
3) ;
3) 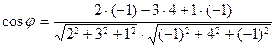 ;
4) ;
4)  ;
5) ;
5) 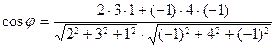
| |
12. Среди уравнений:
1) 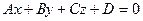 ;
2) ;
2) 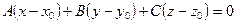 ;
3) ;
3) 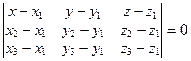 ;
4) ;
4) 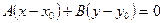 ; 5) ; 5) 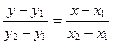 выбрать уравнение плоскости, проходящей через точки
выбрать уравнение плоскости, проходящей через точки 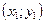 , , 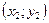 , , 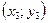 . .
| 1) 5; 2) 4; 3)* 3; 4) 2; 5) 1 | |
13. Расстояние 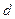 от точки от точки 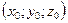 до плоскости до плоскости 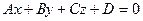 находится по формуле находится по формуле 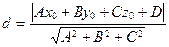 . Для нахождения расстояния от точки . Для нахождения расстояния от точки 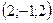 до плоскости до плоскости 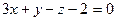 необходимо найти значение выражения: необходимо найти значение выражения:
| 1) 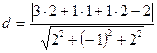 ; 2) ; 2) 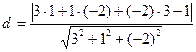 ;
3) ;
3) 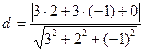 ; 4) ; 4) 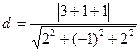 ;
5)* ;
5)* 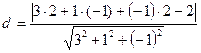
| |
14. Косинус угла 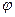 между плоскостями между плоскостями 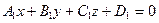 и и 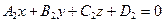 находится по формуле находится по формуле 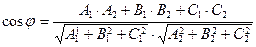 . Для нахождения косинуса угла . Для нахождения косинуса угла 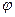 между плоскостями между плоскостями 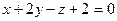 и и 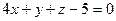 необходимо найти значение выражения: необходимо найти значение выражения:
| 1) 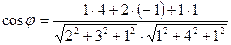 ;
2)* ;
2)* 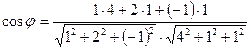 ;
3) ;
3) 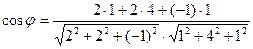 ;
4) ;
4) 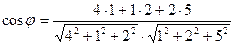 ;
5) ;
5) 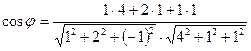
| |
15. Матрица системы линейных уравнений 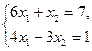 имеет вид: имеет вид:
| 1) 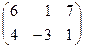 ; 2) ; 2) 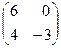 ; 3) ; 3) 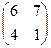 ;
4)* ;
4)* 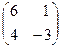 ; 5) ; 5) 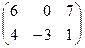
| |
16. Расширенная матрица системы линейных уравнений 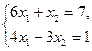 имеет вид: имеет вид:
| 1) 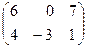 ; 2) ; 2) 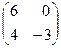 ; 3) ; 3) 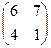 ;
4) ;
4) 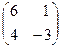 ; 5)* ; 5)* 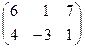
| |
17. При решении системы линейных уравнений  по правилу Крамера определитель по правилу Крамера определитель 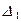 имеет вид: имеет вид:
| 1) 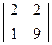 ; 2)* ; 2)*  ; 3) ; 3) 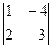 ; 4) ; 4) 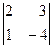 ; 5) ; 5) 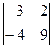
| |
18. При решении системы линейных уравнений  по правилу Крамера определитель по правилу Крамера определитель 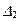 имеет вид: имеет вид:
| 1)* 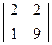 ; 2) ; 2) 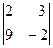 ; 3) ; 3) 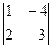 ; 4) ; 4) 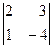 ; 5) ; 5) 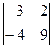
| |
19. Пусть при решении системы линейных уравнений по правилу Крамера получены значения: 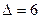 ; ; 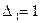 . Тогда значение первой переменной системы равно: . Тогда значение первой переменной системы равно:
| 1) 6; 2) – 1; 3) 1; 4) 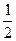 ; 5)* ; 5)* 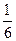
| |
20. Укажите значение переменной 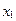 , удовлетворяющее системе линейных уравнений , удовлетворяющее системе линейных уравнений 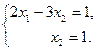
| 1) 1; 2)* 2; 3) 3; 4) 4; 5) 5 | |
21. Укажите область решения системы линейных неравенств с двумя переменными 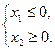
| 1)
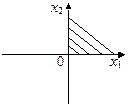
| 2)*
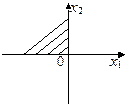
|
3)
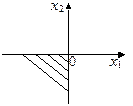
| 4)
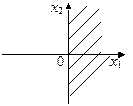
| |
5)
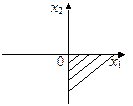
| ||
22. При решении системы линейных уравнений  по правилу Крамера определитель по правилу Крамера определитель 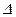 имеет вид: имеет вид:
| 1) 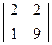 ; 2) ; 2) 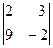 ; 3) ; 3) 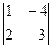 ; 4)* ; 4)* 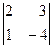 ; 5) ; 5) 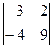
|
Дата добавления: 2015-07-25; просмотров: 80 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тема 1. Аналитическая геометрия на плоскости, векторная алгебра, матрицы | | | Тема 3. Числа и числовые последовательности, числовые ряды |