
Читайте также:
|
| Вопрос | Ответы |
1. Пусть функция 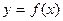 определена на определена на  и во внутренней точке и во внутренней точке  промежутка принимает наибольшее или наименьшее значение. Если существует конечная производная промежутка принимает наибольшее или наименьшее значение. Если существует конечная производная  , то необходимо, чтобы: , то необходимо, чтобы:
| 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  ; 5)* ; 5)* 
|
2. Если 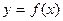 и и  — дифференцируемые бесконечно малые или бесконечно большие функции при — дифференцируемые бесконечно малые или бесконечно большие функции при  , то имеет место равенство (правило Лопиталя): , то имеет место равенство (правило Лопиталя):
| 1)  ; 2) ; 2)  ;
3)* ;
3)*  ; 4) ; 4) 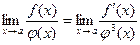 ;
5) ;
5) 
|
3. Пусть функция 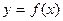 определена на множестве определена на множестве  и внутри его имеет конечную производную и внутри его имеет конечную производную  . Для того, чтобы . Для того, чтобы  была постоянной на была постоянной на  , необходимо и достаточно, чтобы внутри , необходимо и достаточно, чтобы внутри  выполнялось равенство: выполнялось равенство:
| 1)  ;
2)* ;
2)*  ;
3) ;
3)  ;
4) ;
4)  ;
5) ;
5) 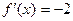
|
4. Точкой экстремума функции  является точка: является точка:
| 1) 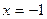 ; 2) ; 2) 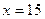 ; 3) ; 3)  ; 4) ; 4) 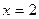 ; 5)* ; 5)* 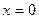
|
5. Если в некотором промежутке производная данной функции 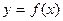 положительна, т.е. положительна, т.е.  , то функция в этом промежутке: , то функция в этом промежутке:
| 1)* возрастает; 2) имеет максимум; 3) убывает; 4) постоянна; 5) имеет минимум |
6. Кривая 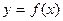 выпукла вверх на интервале выпукла вверх на интервале  , если во всех точках этого интервала выполняется соотношение: , если во всех точках этого интервала выполняется соотношение:
| 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  ; 5)* ; 5)* 
|
7. Точка с абсциссой 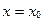 кривой кривой 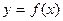 будет точкой перегиба, если будет точкой перегиба, если  или или  не существует и выполняется условие: не существует и выполняется условие:
| 1)  при переходе через точку при переходе через точку 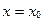 меняет знак;
2) меняет знак;
2)  ;
3) ;
3)  ;
4)* при переходе через точку ;
4)* при переходе через точку 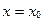 производная производная  меняет знак;
5) меняет знак;
5) 
|
8. Вертикальной асимптотой графика функции  является прямая: является прямая:
| 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4) 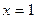 ; 5)* ; 5)* 
|
Дата добавления: 2015-07-25; просмотров: 43 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тема 5. Дифференцирование функции одной переменной | | | Тема 7. Функциональные ряды |