
Читайте также:
|
| Вопрос | Ответы |
1. Предел отношения (если он существует) приращения  функции функции 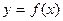 в точке в точке 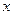 к приращению к приращению 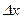 аргумента, при условии, что приращение аргумента аргумента, при условии, что приращение аргумента 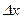 стремится к нулю, т.е. стремится к нулю, т.е.  , называется: , называется:
| 1) непрерывностью 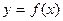 в точке в точке 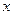 ;
2) приращением аргумента ;
2) приращением аргумента 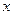 ;
3) приращением функции ;
3) приращением функции 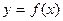 в точке в точке 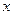 ;
4) *производной функции ;
4) *производной функции 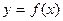 в точке в точке 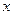 ;
5) пределом функции ;
5) пределом функции 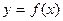 в точке в точке 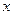
|
2. Если в некоторой точке 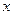 функции функции 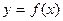 и и  имеют производные, то производная от суммы этих функций имеют производные, то производная от суммы этих функций  равна: равна:
| 1)  ; 2) ; 2)  ; 3) ; 3)  ;
4) ;
4)  ; 5)* ; 5)* 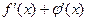
|
3. Если в точке 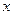 функции функции  и и  имеют производные, то в точке имеют производные, то в точке 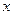 произведение этих функций имеет производную, которая равна: произведение этих функций имеет производную, которая равна:
| 1)  ; 2) ; 2)  ; 3)* ; 3)*  ;
4) ;
4) 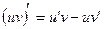 ; 5) ; 5) 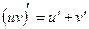
|
4. Производная функции  равна: равна:
| 1)  ; 2) ; 2)  ;
3) ;
3)  ; 4) ; 4)  ; 5)* ; 5)* 
|
5. Угловой коэффициент касательной к графику функции  в точке в точке  равен: равен:
| 1) 4; 2)*  ; 3) ; 3) 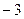 ; 4) –2; 5) 5 ; 4) –2; 5) 5
|
6. Если в точке 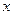 функции функции  и и  имеют производные, причем в этой точке функция имеют производные, причем в этой точке функция  отлична от нуля, то частное этих функций имеет в точке отлична от нуля, то частное этих функций имеет в точке 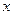 производную, которая вычисляется по формуле: производную, которая вычисляется по формуле:
| 1)  ; 2)* ; 2)*  ; 3) ; 3) 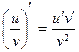 ;
4) ;
4)  ; 5) ; 5) 
|
7. Для нахождения производной функции  в точке в точке  необходимо найти значение выражения: необходимо найти значение выражения:
| 1)  ; 2) ; 2)  ;
3) ;
3)  ; 4) ; 4)  ;
5)* ;
5)* 
|
8. Производная функции  равна: равна:
| 1)  ; 2)* ; 2)*  ; 3) ; 3)  ;
4) ;
4)  ; 5) ; 5) 
|
9. Производная функции  равна: равна:
| 1) 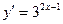 ; 2) ; 2) 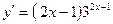 ; 3)* ; 3)*  ;
4) ;
4)  ; 5) ; 5) 
|
10. Производная функции  равна: равна:
| 1)*  ; 2) ; 2)  ; 3) ; 3)  ;
4) ;
4)  ; 5) ; 5) 
|
11. Найти дифференциал функции  . .
| 1)  ; 2) ; 2)  ; 3) ; 3)  ;
4)* ;
4)*  ; 5) ; 5) 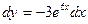
|
12. Эластичность функции 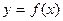 определяется формулой: определяется формулой:
| 1)  ; 2) ; 2) 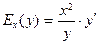 ; 3) ; 3)  ;
4) ;
4)  ; 5)* ; 5)* 
|
Дата добавления: 2015-07-25; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тема 4. Функции одной переменной, непрерывные функции одной переменной | | | Тема 6. Основные теоремы о функции одной переменной, исследование функции с помощью производной, экстремумы |