
|
Читайте также: |
| Вопрос | Ответы |
| 1. Третьей четверти декартовой прямоугольной системе координат на плоскости принадлежит точка: | 1)  ; 2)* ; 2)* 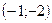 ; 3) ; 3) 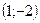 ; 4) ; 4) 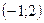 ; 5) ; 5) 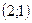
|
2. Середина отрезка с концами 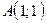 и и 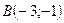 находится в точке: находится в точке:
| 1) 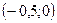 ; 2) ; 2) 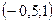 ; 3) ; 3) 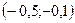 ; 4)* ; 4)* 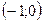 ; 5) ; 5) 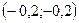
|
3. Прямая 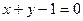 пересекает координатную ось пересекает координатную ось 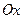 в точке: в точке:
| 1) 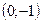 ; 2) ; 2) 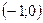 ; 3)* ; 3)* 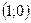 ; 4) ; 4) 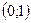 ; 5) ; 5) 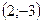
|
4. Прямая 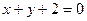 пересекает координатную ось пересекает координатную ось 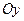 в точке: в точке:
| 1)* 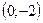 ; 2) ; 2) 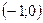 ; 3) ; 3) 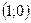 ; 4) ; 4) 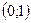 ; 5) ; 5) 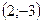
|
5. Прямая 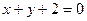 проходит через точку: проходит через точку:
| 1) 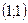 ; 2) ; 2)  ; 3)* ; 3)* 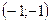 ; 4) ; 4) 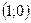 ; 5) ; 5) 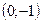
|
6. Нормальным вектором прямой 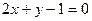 является вектор с координатами: является вектор с координатами:
| 1) 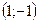 ; 2) ; 2)  ; 3) ; 3) 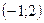 ; 4)* ; 4)* 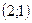 ; 5) ; 5) 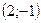
|
7. Угловой коэффициент прямой 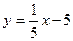 равен: равен:
| 1) 1; 2) 5; 3) 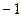 ; 4) ; 4) 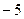 ; 5)* ; 5)* 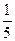
|
8. У прямой, перпендикулярной данной прямой 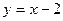 , угловой коэффициент равен: , угловой коэффициент равен:
| 1) 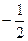 ; 2) ; 2) 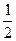 ; 3) 2; 4)* ; 3) 2; 4)* 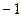 ; 5) ; 5) 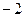
|
9. У прямой, параллельной данной прямой 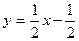 , угловой коэффициент равен: , угловой коэффициент равен:
| 1) 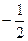 ; 2)* ; 2)* 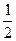 ; 3) 2; 4) ; 3) 2; 4) 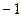 ; 5) ; 5) 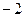
|
10. Среди уравнений:
1) 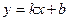 , 2) , 2) 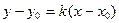 ,
3) ,
3) 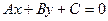 , 4) , 4) 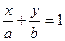 ,
5) ,
5) 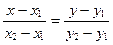 выбрать уравнение прямой по заданному угловому коэффициенту
выбрать уравнение прямой по заданному угловому коэффициенту 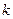 и проходящей через данную точку и проходящей через данную точку 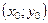 . .
| 1) 5; 2) 4; 3) 3; 4)* 2; 5) 1. |
11. Среди уравнений:
1) 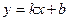 , 2) , 2) 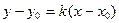 ,
3) ,
3) 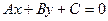 , 4) , 4) 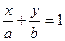 ,
5) ,
5) 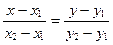 выбрать уравнение прямой, проходящей через две данные точки
выбрать уравнение прямой, проходящей через две данные точки 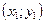 , , 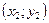 . .
| 1)* 5; 2) 4; 3) 3; 4) 2; 5) 1. |
12. Среди уравнений:
1) 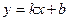 , 2) , 2) 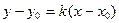 ,
3) ,
3) 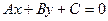 , 4) , 4) 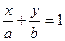 ,
5) ,
5) 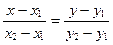 выбрать уравнение прямой в отрезках по осям
выбрать уравнение прямой в отрезках по осям 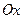 и и 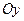 . .
| 1) 5; 2)* 4; 3) 3; 4) 2; 5) 1. |
13. Тангенс угла 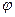 между прямыми между прямыми 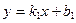 и и 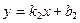 находится по формуле находится по формуле 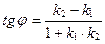 . Для нахождения тангенса угла . Для нахождения тангенса угла 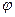 между прямыми между прямыми 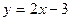 и и 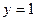 необходимо найти значение выражения: необходимо найти значение выражения:
| 1) 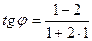 ; 2)* ; 2)* 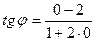 ; 3) ; 3) 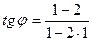 ;
4) ;
4) 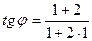 ; 5) ; 5) 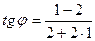
|
14. Расстояние 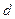 от точки от точки 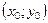 до прямой до прямой 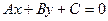 находится по формуле находится по формуле 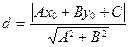 . Для нахождения расстояния от точки . Для нахождения расстояния от точки 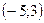 до прямой до прямой 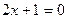 необходимо найти значение выражения: необходимо найти значение выражения:
| 1) 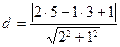 ; 2)* ; 2)* 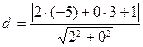 ;
3) ;
3) 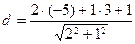 ; 4) ; 4) 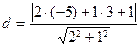 ;
5) ;
5) 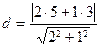
|
15. Прямые 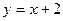 и и 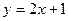 пересекаются в точке: пересекаются в точке:
| 1) 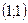 ; 2) ; 2)  ; 3) ; 3) 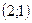 ; 4) ; 4) 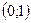 ; 5)* ; 5)* 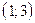
|
16. Большая полуось эллипса 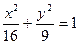 равна: равна:
| 1)* 4; 2) 9; 3) 2; 4) 3; 5) 16 |
17. Малая полуось эллипса 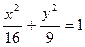 равна: равна:
| 1) 4; 2) 9; 3) 2; 4)* 3; 5) 16 |
18. Действительная полуось гиперболы 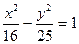 равна: равна:
| 1)* 4; 2) 9; 3) 25; 4) 10; 5) 5 |
19. Действительная полуось гиперболы 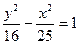 равна: равна:
| 1) 16; 2) 9; 3) 25; 4)* 4; 5) 5 |
20. Мнимая полуось гиперболы 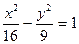 равна: равна:
| 1)* 3; 2) 9; 3) 25; 4) 5; 5) 16 |
21. Мнимая полуось гиперболы 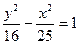 равна: равна:
| 1) 3; 2)* 5; 3) 9; 4) 25; 5) 16 |
22. Центр окружности 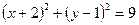 находится в точке: находится в точке:
| 1) 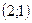 ; 2)* ; 2)* 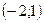 ; 3) ; 3) 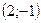 ; 4) ; 4) 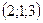 ; 5) 3 ; 5) 3
|
23. Радиус окружности 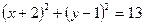 равен: равен:
| 1) 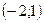 ; 2) 13; 3) 1; 4) 9; 5)* ; 2) 13; 3) 1; 4) 9; 5)* 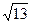
|
24. Параметр 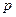 параболы, задаваемой уравнением параболы, задаваемой уравнением 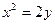 , равен: , равен:
| 1)* 1; 2) 2; 3) 0; 4) 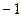 ; 5) ; 5) 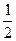
|
25. Даны векторы 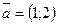 и и 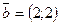 . Найти координаты вектора . Найти координаты вектора 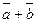 . .
| 1) 3; 2) 11; 3) 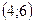 ; 4)* ; 4)* 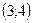 ; 5) 10 ; 5) 10
|
26. Среди уравнений:
1) 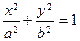 , 2) , 2) 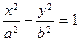 , 3) , 3) 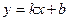 ,
4) ,
4) 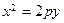 , 5) , 5) 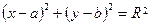 выбрать уравнение, задающее на координатной плоскости
выбрать уравнение, задающее на координатной плоскости 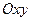 параболу. параболу.
| 1) 1; 2) 2; 3) 3; 4)* 4; 5) 5 |
27. Даны векторы 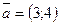 и и 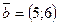 . Найти координаты вектора . Найти координаты вектора 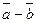 . .
| 1) 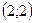 ; 2) ; 2) 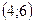 ; 3) 4; 4) ; 3) 4; 4) 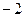 ; 5)* ; 5)* 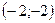
|
28. Длина вектора 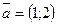 равна: равна:
| 1) 1; 2) 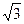 ; 3) 2; 4) ; 3) 2; 4) 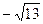 ; 5)* ; 5)* 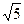
|
29. Скалярное произведение векторов 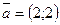 и и 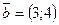 равно: равно:
| 1)* 14; 2) 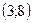 ; 3) 11; 4) ; 3) 11; 4) 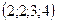 ; 5) ; 5) 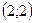
|
30. Даны точки 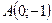 и и 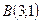 . Найти координаты вектора . Найти координаты вектора 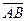 . .
| 1) 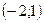 ; 2)* ; 2)* 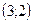 ; 3) ; 3) 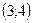 ; 4) ; 4) 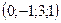 ; 5) ; 5) 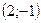
|
31. Дан вектор  . Найти координаты вектора . Найти координаты вектора 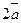 . .
| 1) 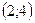 ; 2) 6; 3) ; 2) 6; 3) 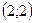 ; 4) ; 4) 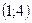 ; 5)* ; 5)* 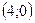
|
32. Произведение элементов 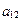 и и 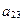 матрицы матрицы 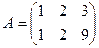 равно: равно:
| 1) 5; 2)* 18; 3) 12; 4) 16; 5) 8 |
33. Произведение элементов главной диагонали матрицы 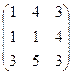 равно: равно:
| 1) 9; 2) 18; 3) 12; 4)* 3; 5) 8 |
34. Дана матрица 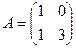 . Найти матрицу . Найти матрицу 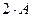 . .
| 1)* 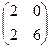 ; 2) ; 2) 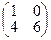 ; 3) ; 3) 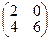 ; 4) ; 4) 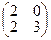 ; 5) ; 5) 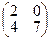
|
35. Даны матрицы 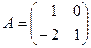 и и 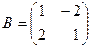 . Найти матрицу . Найти матрицу 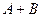 , если она существует. , если она существует.
| 1) 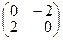 ; 2) ; 2) 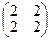 ; 3)* ; 3)* 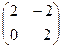 ; 4) ; 4) 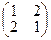 ; 5) не существует ; 5) не существует
|
36. Даны матрицы 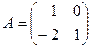 и и 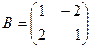 . Найти матрицу . Найти матрицу 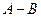 , если она существует. , если она существует.
| 1) 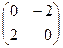 ; 2)* ; 2)* 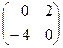 ; 3) ; 3) 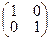 ; 4) ; 4) 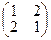 ; 5) не существует ; 5) не существует
|
37. Даны матрицы 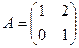 и и 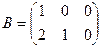 . Найти матрицу . Найти матрицу 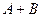 , если она существует. , если она существует.
| 1) 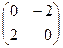 ; 2) ; 2) 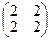 ; 3) ; 3) 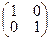 ; 4) ; 4) 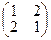 ; 5)* не существует ; 5)* не существует
|
38. Даны матрицы 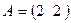 и и 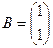 . Найти матрицу . Найти матрицу 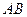 , если она существует. , если она существует.
| 1) 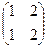 ; 2) ; 2) 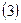 ; 3)* ; 3)* 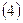 ; 4) ; 4) 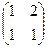 ; 5) не существует ; 5) не существует
|
39. Если 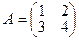 , то произведение элементов второй строки транспонированной матрицы , то произведение элементов второй строки транспонированной матрицы 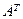 равно: равно:
| 1) 4; 2) 3; 3) 2; 4)* 8; 5) 12 |
40. Определитель 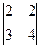 равен: равен:
| 1) 4; 2) 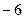 ; 3)* 2; 4) 5; 5) ; 3)* 2; 4) 5; 5) 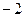
|
41. Определитель 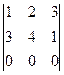 равен: равен:
| 1) 1; 2) 2; 3) 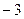 ; 4) 9; 5)* 0 ; 4) 9; 5)* 0
|
42. Определитель 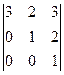 равен: равен:
| 1)* 3; 2) 4; 3) 1; 4) 7; 5) 2 |
43. Минор 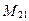 элемента элемента 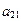 определителя матрицы определителя матрицы 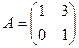 равен: равен:
| 1) 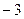 ; 2) 2; 3) 1; 4)* 3; 5) 0 ; 2) 2; 3) 1; 4)* 3; 5) 0
|
44. Алгебраическое дополнение 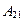 элемента элемента 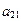 определителя матрицы определителя матрицы 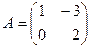 равно: равно:
| 1) 1; 2) 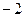 ; 3) 0; 4) 2; 5)* 3 ; 3) 0; 4) 2; 5)* 3
|
Дата добавления: 2015-07-25; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основы реабилитации, физиотерапии, лечебной физкультуры и массажа | | | Тема 2. Квадратичные формы, элементы аналитической геометрии в пространстве, системы линейных уравнений и неравенств |