
Читайте также:
|
При скользящем усреднении берется суммарный спрос за ограниченное число отрезков в прошлом, который делится на число этих отрезков. Для каждого последующего периода скользящее среднее вычисляется заново, при этом учитываются количественные показатели для отрезков времени непосредственного предшествующих периоду, для которого составляет прогноз, то есть
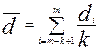
где m - последний из отрезков времени, для которого известен уровень спроса;
к - количество отрезков времени, содержащихся во временном интервале, ассоциированным с разрабатываемым прогнозом.
Следует подчеркнуть, что при этом всегда пытаются учесть наиболее свежие данные. Поэтому прогнозируемое среднее значение спроса относится к
 |
(m+1)- му периоду, то есть d=dm+1
Обратимся к рассматриваемой ситуации. Выделим в каждом случае из предыдущего периода пять последних месяцев. Получим
dXIII = (233+219+234+219+220) / 5 = 225 ед.;
dXIV = (219+234+219+220+225) / 5 = 223 ед.
dXV = (234+219+220+225+223) / 5 = 224 ед.
dXVI = (219+220+225+223+224) / 5 = 222 ед.
dXVII = (220+225+223+224+222) / 5 = 223 ед.
dXVIII = (225+223+224+222+223) / 5 = 223 ед.
По остальным шести месяцам прогнозируемого периода величина скользящего среднего равна 223 ед.
Оценка погрешности прогноза производится обычным образом. Следует иметь в виду, что стандартное отклонение должно на каждом шаге вычисляется заново, т.е.
|
| dt | 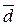 =225 =225
| |||||
 dt-d dt-d
| -6 | -6 | -5 | - | ||
 (dt-d)2 (dt-d)2
| å 242 |
Для следующего шага:

| 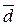 =223 =223
| |||||||
 dt-d dt-d
| -4 | -4 | -3 | - | ||||
| (dt-d)2 | å 166 |
и т.д.
Сравним скользящее среднее с результатами, полученными путем использования других прогностических функций:
среднее арифметическое - 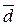 = 213 ± 12; Sdt = 12;
= 213 ± 12; Sdt = 12;
линейная прогнозирующая функция - 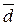 = 213; Sdt = 7;
= 213; Sdt = 7;
нелинейная прогнозирующая функция - 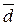 = 211; Sdt = 13;
= 211; Sdt = 13;
То есть, мы видим, что прогнозы близки, но могут и существенно отличаться.
Прогнозы, полученные методом скользящего среднего менее надежны по сравнению с рассмотренными статическими методами и могут охватывать лишь ближайший отрезок времени.
Дата добавления: 2015-07-25; просмотров: 50 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисления, сопровождающие построение функции гиперболы. | | | Спрос, прогнозируемый методом экспоненциального сглаживания |