Алгоритм вычисления показателей и экономический анализ полученных результатов

1. В качестве изучаемой системы берется экономика условного объекта.

2. Используя табличный редактор Excel, рассчитываем по формуле (9) зависимость Y = f₁(t) при отсутствии потребления, т.е. C(t) = 0. Значения коэффициента приростной капиталоемкости В и Y(0) приведены в таблице исходных данных. Величину t задаём в пределах от 0 до 20 лет с интервалом Dt = 1 году. Полученные результаты записаны в таблице 2.

Таблица 2

t	Y(t) = f1(t)
	425,28975
	502,42047
	593,53966
	701,18425
	828,35132
	978,58146
	1156,0574
	1365,7204
	1613,4081
	1906,0164
	2251,6923
	2660,0602
	3142,4898
	3712,4131
	4385,6978
	5181,0898
	6120,7344
	7230,7933
	8542,1729
	10091,385

Затем, применив "Мастер диаграмм" табличного редактора Excel, строим график зависимости Y = f₁(t) (Приложение 1).

По графику Y = f₁(t) можно сделать вывод, что в этом случае все ресурсы направляются на инвестиции, в результате чего могут быть определены максимальные технически возможные темпы роста дохода. Непрерывный темп прироста равен (1/6). Это максимально возможный (технологический) темп прироста дохода в рассматриваемой экономической системе.

3. Аналогично производим расчеты значений трех функций Y = f(t) по формуле (13) для трех случаев C(0) при постоянной функции потребления, т.е. C(t) = C(0) = const. Численные значения C(0) для каждого случая берём из таблицы 1.

Полученные результаты записаны в таблице 3.

Таблица 3

Y(t) = f2(t)	Y(t) = f3(t)	Y(t) = f4(t)
389,0176661	370,8816248
423,297988	383,7367455
463,7954033	398,9232762
511,6374466	416,8640425
568,1561425	438,0585535
634,9250926	463,0969097
713,8032869	492,6762326
806,9868631	527,6200737
917,0702513	568,9013442
1047,118408	617,669403
1200,752152	675,2820571
1382,248976	743,3433659
1596,662138	823,7483018
1849,96136	918,7355101
2149,199034	1030,949638
2502,706575	1163,514966
2920,32639	1320,122396
3413,685908	1505,132215
3996,521311	1723,695492
4685,059983	1981,897494

Применив "Мастер диаграмм" табличного редактора Excel, строим на одной диаграмме графики зависимостей: Y = f₂(t), Y = f₃(t), Y = f₄(t), С = f₅(t), С = f₆(t), С = f₇(t) (Приложение 2).

По графикам Y = f₂(t) и С = f₅(t), Y = f₃(t) и С = f₆(t) можно сделать вывод, что с ростом времени растет доход Y(t), а потребление C(t) = const. В связи с этим непрерывный темп прироста дохода v(t) возрастая, стремится к при , так как доход растёт, а постоянный объём потребления составляет всё меньшую его долю. Также можно отметить, что графики Y = f₂(t), Y = f₃(t), С = f₅(t), С = f₆(t) ниже Y = f₁(t) на величину потребления.

Необходимо также отметить, что при C(0) = Y(0) непрерывный темп прироста дохода равен нулю и, следовательно, роста дохода вообще не происходит.

4. Для функции потребления, растущей с постоянным темпом:

(22)

рассчитываем значения темпов роста r для трех различных значений C(0) по формуле:

(23)

Величины B, Y(0) и C(0) выбираются из таблицы исходных данных.

Получаем:

r1	r2	r3
0,08	0,03

5. Для каждого полученного значения r рассчитываем значения С = f₈(t), С = f₉(t), С = f₁₀(t), используя формулу (22), и значения Y = f₁₁(t), Y = f₁₂(t), Y = f₁₃(t), используя формулу (19). Значения t задаём в пределах от 0 до 30 лет с интервалом Dt = 1 году. Результаты приведены в таблице 4.

С помощью "Мастера диаграмм" табличного редактора Excel, строим на одной диаграмме графики зависимостей: С = f₈(t), С = f₉(t), С = f₁₀(t), Y = f₁₁(t), Y = f₁₂(t), Y = f₁₃(t) (Приложение 3).

Таблица 4

C = f8(t)	C = f9(t)	C = f10(t)	Y = f11(t)	Y = f12(t)	Y = f13(t)
215,3773144	308,4501532		387,6791659	370,1401839
231,9369378	317,1383234		417,486488	380,5659881
249,7697738	326,0712149		449,5855928	391,2854578
268,9737155	335,2557206		484,1526879	402,3068647
289,6541824	344,698928		521,3775283	413,6387136
311,9246995	354,4081239		561,4644591	425,2897486
335,9075204	364,3908004		604,6335367	437,2689604
361,7342981	374,6546607		651,1217366	449,5855928
389,5468082	385,207625		701,1842548	462,24915
419,4977269	396,0578365		755,0959084	475,2694038
451,751469	407,2136679		813,1526443	488,6564015
486,4850909	418,6837275		875,6731635	502,420473
523,8892618	430,4768664		943,0006712	516,5722396
564,1693112	442,6021846		1015,50476	531,1226216
607,5463555	455,0690389		1093,58344	546,0828467
654,2585121	467,8870493		1177,665322	561,4644591
704,5622062	481,0661068		1268,211971	577,2793282
758,7335789	494,6163812		1365,720442	593,5396575
817,0700028	508,5483286		1470,726005	610,2579943
879,8917144	522,8726996		1583,805086	627,4472395
947,5435719	537,6005477		1705,578429	645,1206572
1020,396949	552,7432377		1836,714508	663,2918853
1098,851772	568,3124546		1977,93319	681,9749455
1183,338718	584,3202123		2130,009693	701,1842548
1274,321576	600,7788634		2293,778836	720,9346361
1372,299793	617,7011083		2470,139627	741,2413299
1477,81122	635,100005		2660,060196	762,120006
1591,435058	652,9889795		2864,583105	783,5867754
1713,795044	671,381836		3084,83108	805,6582032
1845,56287	690,2927673		3322,013167	828,3513207

По графикам С = f₈(t) и Y = f₁₁(t) [С = f₉(t) и Y = f₁₂(t)], когда r₁ = 0,08 [r₂=0,03], причем r < 1/B (0,08 < 0,17 [0,03 < 0,17]), можно сделать вывод, что темп прироста дохода равен темпу прироста потребления. Норма накопления в этом случае постоянна во времени и равна , а темп прироста дохода пропорционален норме накопления и обратно пропорционален приростной капиталоёмкости. Именно эта модификация модели экономического роста, в которой постоянна норма накопления, называется моделью Харрода-Домара.

Из графиков С = f₁₀(t) и Y = f₁₃(t) следует,что когда Y(0) = C(0), согласно формуле (20), величина a₀ = 0. Следовательно, для модели Харрода-Домара r также будет равно нулю. В формуле (19) первое слагаемое станет равным нулю, а второе слагаемое будет равно Y(0) для всех значений t, т.е. Y(t) = Y(0) = const.

6. Рассчитываем значения темпов роста функции C(t) для трех различных значений C(0) по формуле:

. (24)

Получаем:

r1	r2	r3
0,093	0,035

7. Используя формулы (22) и (19), для каждого значения найденного r, рассчитываем зависимости: С = f₁₄(t), С = f₁₅(t), С = f₁₆(t), Y = f₁₇(t), Y = f₁₈(t), Y = f₁₉(t) и строим на одной диаграмме графики этих функций (Приложение 4). Полученные результаты занесены в таблицу 5.

Таблица 5

C = f14(t)	C = f15(t)	C = f16(t)	Y = f17(t)	Y = f18(t)	Y = f19(t)
219,4029425	310,599623		387,3341834	369,9526949
240,6882558	321,5737527		415,9434573	379,7552416
264,0385577	332,9356211		445,7018404	389,3113289
289,6541824	344,698928		476,4258467	398,5047377
317,7548996	356,8778569		507,8606938	407,1956445
348,5817997	369,4870927		539,6636848	415,2162509
382,3993627	382,541839		571,3842173	422,3656179
419,4977269	396,0578365		602,439775	428,4035597
460,1951782	410,0513824		632,0871346	433,0434269
504,840881	424,5393492		659,3878777	435,943577
553,8178738	439,539206		683,1671304	436,6972948
607,5463555	455,0690389		701,964251	434,820881
666,4872904	471,1475731		713,9739506	429,7395759
731,1463631	487,7941952		716,9760519	420,7709276
802,0783172	505,0289771		708,2517572	407,1051381
879,8917144	522,8726996		684,4839087	387,7818419
965,2541559	541,3468779		641,6382561	361,6626679
1058,89801	560,4737872		574,8221996	327,3988211
1161,626696	580,27649		478,1168285	283,3927795
1274,321576	600,7788634		344,3773046	227,75304
1397,949517	622,0056282		164,9957361	158,2406512
1533,571187	643,9823788		-70,3803896	72,20604478
1682,350154	666,7356135		-374,1824124	-33,4855955
1845,56287	690,2927673		-761,3170445	-162,542505
2024,609621	714,6822442		-1249,636728	-319,350507
2221,026541	739,933452		-1860,497374	-509,09608
2436,498792	766,0768374		-2619,419535	-737,911746
2672,875021	793,1439229		-3556,871988	-1013,04784
2932,183223	821,1673448		-4709,200171	-1343,07544
3216,648134	850,1808923		-6119,726017	-1738,1261

По графикам С = f₁₄(t) и Y = f₁₇(t) [С = f₁₅(t) и Y = f₁₈(t)], когда (0,17 > 0,093 > 0,08 [0,17 > 0,035 > 0,03]), можно сделать вывод, что темп прироста потребления в этом случае оказывается слишком высоким для экономики. В этом случае коэффициент в формуле (19) отрицателен, так как 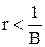, и по той же причине первое отрицательное слагаемое с ростом времени превысит второе. Это приводит к тому, что темп прироста дохода падает и становится с некоторого момента отрицательным, а через некоторое время и сам доход становится равным нулю. После этого модель теряет экономический смысл.

Из графиков С = f₁₆(t) и Y = f₁₉(t) видно, когда Y(0) = C(0), если увеличивать величину темпа прироста потребления r, используя формулу (21), то согласно формуле (20), величина a₀ = 0. Следовательно, для модели Харрода-Домара r также будет равно нулю. В формуле (19) первое слагаемое станет равным нулю, а второе слагаемое будет равно Y(0) для всех значений t, т.е. Y(t) = Y(0) = const.

8. Для случая, когда , т.е. 0,33, рассчитываем по формуле (22) значения С = f₂₀(t), С = f₂₁(t), С = f₂₂(t) и по формуле (19) значения Y = f₂₃(t), Y = f₂₄(t), Y = f₂₅(t), t задаём в пределах от 0 до 30 лет с интервалом Dt = 1 году. В таблице 6 приведены полученные значения:

Таблица №6

C = f20(t)	C = f21(t)	C = f22(t)	Y = f23(t)	Y = f24(t)	Y = f25(t)
279,122485	418,6837	502,4205	382,4393	361,0141	348,159
389,546808	584,3202	701,1843	391,9961	336,784	303,6567
543,656366	815,4845	978,5815	379,6275	272,6715	208,4979
758,733579	1138,1	1365,72	331,9975	147,4041	36,64807
1058,89801	1588,347	1906,016	229,6485	-69,7029	-249,314
1477,81122	2216,717	2660,06	44,4266	-422,651	-702,897
2062,4517	3093,678	3712,413	-264,14	-974,239	-1400,3
2878,38322	4317,575	5181,09	-753,929	-1813,75	-2449,65
4017,10738	6025,661	7230,793	-1507,36	-3067,75	-4003,98
5606,32498	8409,487	10091,38	-2641,41	-4915,12	-6279,35
7824,2568	11736,39	14083,66	-4321,62	-7608,28	-9580,28
10919,63	16379,45	19655,33	-6781,76	-11502,7	-14335,2
15239,5713	22859,36	27431,23	-10351,3	-17098,1	-21146,2
21268,5351	31902,8	38283,36	-15493,7	-25096,7	-30858,5
29682,6318	44523,95	53428,74	-22860,4	-36483,5	-44657,3
41425,4498	62138,17	74565,81	-33366	-52639,5	-64203,6
57813,8724	86720,81		-48292,7	-75499,5	-91823,5
80685,7587	121028,6	145234,4	-69437,9	-107772	-130773
112606,047	168909,1	202690,9	-99318,2	-153248	-185607
157154,399	235731,6	282877,9	-141457	-217231	-262695
219326,632	328989,9	394787,9	-200782	-307134	-370945
306094,972	459142,5		-284187	-433322	-522804
427189,947	640784,9	768941,9	-401309	-610282	-735666
596191,597	894287,4		-565617	-858253	-1033834
832052,401			-795932	-1205509	-1451254
1161222,67			-1118552	-1691543	-2035338
1620616,79			-1570207	-2371514	-2852298
2261752,92			-2202201	-3322443	-3994589
3156530,48			-3086178	-4651881	-5591302
4405293,16			-4322182	-6509987	-7822670

Применив "Мастер диаграмм" табличного редактора Excel, строим на одной диаграмме графики этих зависимостей (Приложение 5).

По графикам С = f₂₀(t) и Y = f₂₃(t), С = f₂₁(t) и Y = f₂₄(t), С = f₂₂(t) и Y = f₂₅(t) видно, когда (в нашем случае ), то потребление будет занимать всё большую часть дохода, что сведёт к нулю сначала инвестиции, а затем и доход. Это также видно из формулы (19) решения модели. Действительно, если , то коэффициент отрицателен, а растёт быстрее, чем , следовательно, отрицательное второе слагаемое через некоторое время перевесит первое.

Дата добавления: 2015-07-25