Постановка задачи

Модель макроэкономической динамики Харрода-Домара описывает динамику взаимосвязи основных макроэкономических показателей закрытой экономики. При этом доход равен сумме объема потребления и инвестиций :

. (1)

Так как экономика считается закрытой, поэтому чистый экспорт равен нулю и государственные расходы в модели не выделяются. Основное соотношение в модели Харрода-Домара - это взаимосвязь между инвестициями и скоростью роста дохода. Предполагается, что скорость роста дохода пропорциональна инвестициям:

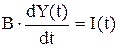, (2)

где – коэффициент приростной капиталоёмкости, или капиталоёмкости прироста дохода, а обратная величина: b= 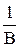называется приростной капиталоотдачей.

При построении модели приняты следующие допущения:

1. Инвестиционный лаг равен нулю и, следовательно, инвестиции мгновенно переходят в прирост капитала:

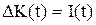(3)

где 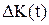- непрерывная функция прироста капитала во времени.

2. Выбытие капитала отсутствует.

3. Производственная функция в модели линейна. Это вытекает из пропорциональности прироста дохода приросту капитала, так как

, (4)

и, следовательно: 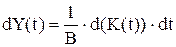. (5)

Однако линейная производственная функция:

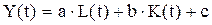, (6)

где ,

обладает этим свойством, если либо , либо . Из данных положений вытекают следующие допущения модели:

1. Затраты труда постоянны во времени либо выпуск не зависит от затрат труда, поскольку труд не является дефицитным ресурсом;

2. Модель не учитывает влияния на объем выпуска продукции научно-технического прогресса.

В модели Харрода-Домара предполагается, что динамика объёма потребления задаётся экзогенно. Этот показатель может считаться постоянным во времени, расти с заданным постоянным темпом или иметь какую-либо другую динамику

1) Простейший вариант модели получается, если считать . В этом случае все ресурсы экономики направляются на инвестиции, в результате чего могут быть определены максимальные технически возможные темпы роста дохода и модель, учитывая (1), (2) принимает следующий вид:

(7)

Представив (7) в стандартном виде, получим:

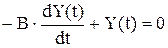. (8)

Выражение (8) – однородное линейное дифференциальное уравнение, решение которого имеет вид:

. (9)

Непрерывный темп прироста равен . Это максимально возможный (технологический) темп прироста дохода в рассматриваемой экономической системе.

2) Если , то получаем:

(10)

или, сделав перестановку членов уравнения, получим:

. (11)

Это - неоднородное линейное дифференциальное уравнение и его частное решение имеет вид: . Складывая частное решение уравнения (11) с общим решением однородного уравнения 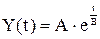, получаем его общее решение:

. (12)

Подставив в (12) , получим 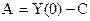, следовательно, общее решение уравнения (11) будет следующим:

. (13)

Непрерывный темп прироста дохода 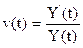для уравнения (11) получим из следующего выражения:

. (14)

Следовательно, непрерывный темп прироста дохода равен:

. (15)

Он составляет: в начальный момент времени, при . С ростом времени растет доход Y(t), а потребление С(t) = const. В связи с этим v(t) возрастая, стремится к при , так как доход растёт, а постоянный объём потребления составляет всё меньшую его долю. Величина в скобках:

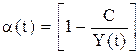(16)

является нормой накопления в момент времени . Темп прироста дохода пропорционален этой величине, как и показателю приростной капиталоотдачи b.

При прочих равных условиях рост нормы накопления пропорционально увеличивает темпы прироста дохода. Необходимо также отметить, что при C(0) = Y(0) непрерывный темп прироста дохода равен нулю и, следовательно, роста дохода вообще не происходит.

3) При исследовании варианта модели с показателем потребления , растущим с постоянным темпом , т.е. дифференциальное уравнение модели принимает вид:

(17)

Приведём данное уравнение к стандартному виду:

. (18)

Это - неоднородное линейное дифференциальное уравнение. Решение этого уравнения имеет вид:

. (19)

Согласно экономическому смыслу ясно, что темп прироста потребления не должен быть больше максимально возможного общего темпа прироста 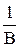. Иначе потребление будет занимать всё большую часть дохода, что сведёт к нулю сначала инвестиции, а затем и доход. Это также видно из формулы (19) решения модели. Действительно, если (например, ),то коэффициент отрицателен, а растёт быстрее, чем , следовательно, отрицательное второе слагаемое через некоторое время перевесит первое.

При 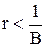, вид решения в рассматриваемой модели во многом зависит от соотношения между показателями и . Величина a - это норма накопления в начальный момент времени . Значение a определяется по формуле (16):

(20)

Если , то темп прироста дохода равен темпу прироста потребления. Норма накопления в этом случае постоянна во времени и равна , а темп прироста дохода пропорционален норме накопления и обратно пропорционален приростной капиталоёмкости. Именно эта модификация модели экономического роста, в которой постоянна норма накопления, называется моделью Харрода-Домара.

Если в рассматриваемой модели , то темп прироста потребления оказывается слишком высоким для экономики. В этом случае коэффициент в формуле (19) отрицателен, так как 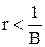, и по той же причине первое отрицательное слагаемое с ростом времени превысит второе. Это приводит к тому, что темп прироста дохода падает и становится с некоторого момента отрицательным, а через некоторое время и сам доход становится равным нулю. После этого модель теряет экономический смысл.

3) случай, когда Y(0) = C(0).

При этом, согласно формуле (20), величина a₀ = 0. Следовательно, для модели Харрода-Домара r также будет равно нулю. В формуле (19) первое слагаемое станет равным нулю, а второе слагаемое будет равно Y(0) для всех значений t, т.е. Y(t) = Y(0) = const. Если же увеличивать величину темпа прироста потребления r, используя формулу:

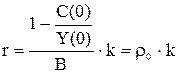, (21)

где k – увеличивающий коэффициент, то при сохранении условия:Y(0) = C(0) имеем тот же результат.

Таким образом, для получения самоподдерживающегося роста дохода в модели Харрода-Домара необходимо в первоначальный момент иметь превышение дохода над потреблением и чем выше это превышение, тем выше темп прироста дохода.

Исходные данные приведены в таблице 1.

Таблица 1

Дата добавления: 2015-07-25