Влияние межъядерного расстояния. Энергии всех состояний молекулы зависят от расстояния между ядрами

Энергии всех состояний молекулы зависят от расстояния между ядрами, которое входит в выражения для кулоновского и обменного интегралов, а также интеграла перекрывания.

Зависимость величины кулоновского (J) и обменного (K) интегралов от межъядерного расстояния в молекуле водорода

Проведя множество расчетов для серии межъядерных расстояний, можно построить зависимость E = f (r _ab), график которой имеет следующий вид:

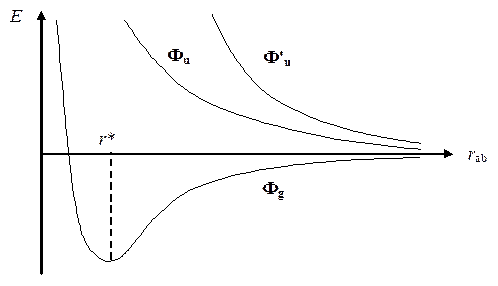
Из графика ясно видно, что процесс сближения двух атомов может приводить к двум принципиально разным результатам. Первый (Ф_g) — возникновение сил притяжения, что сопровождается уменьшением полной энергии системы по мере сближения атомов. Второй (Ф_u и Ф'_u) — возникновение сил отталкивания, что сопровождается возрастанием полной энергии системы. Ясно, что в первом случае сближение атомов будет происходить самопроизвольно до достижения состояния устойчивого равновесия с минимальной энергией (r _ab = r *).

Именно этот случай соответствует образованию химической связи между атомами. Полезно также обратить внимание на то, что образование химической связи сопровождается спариванием электронов атомов (состояние Ф_g синглетное), тогда как возникновение сил отталкивания наблюдается для триплетного состояния Ф_u, когда электроны не спарены. Можно сказать, что спаривание валентных электронов является необходимым признаком химического взаимодействия атомов.

Этот признак, однако, недостаточен, поскольку в состоянии Ф'_u электроны спарены, но химического взаимодействия не наблюдается. Причина такого различия заключается в различной форме электронного облака. Если сравнить пространственные части двух синглетных волновых функций:

Ф_g = AB + BA и Ф'_u = AA – BB

то обнаружится, что во втором случае в электронном облаке имеется разрыв (узловая поверхность, проходящая между ядрами):

Следовательно, для образования химической связи кроме спаривания необходимо еще одно условие — надлежащее распределение электронной плотности в пространстве.

Дата добавления: 2015-07-20