
|
Читайте также: |
Молекула водорода имеет весьма высокую пространственную симметрию. Очевидно, что электронная оболочка также должна быть симметричной, поскольку поведение электронов определяется природой ядер.
Плотность электронного облака определяется квадратом волновой функции. Ясно, что в пространственно симметричных (относительно ядерного остова) точках эти квадраты должны быть равны между собой, а значения самой волновой функции в симметричных точках могут отличаться только знаком. Таким образом, при действии любого из операторов пространственной симметрии на волновую функцию она должна переходить сама в себя; при этом волновая функция может вся целиком умножаться на +1 или –1. Следовательно, для молекулы водорода возможно всего два типа электронных состояний:
пространственно симметричные F [ Фs ] = (+1) × Фs
пространственно антисимметричные F [ Фas ] = (–1) × Фas
Для молекулы водорода в качестве операции симметрии чаще всего используют инверсию (i). Соответственно, волновые функции подразделяются на:
четные (симметричные), для которых i [ Фg ] = (+1) × Фg
нечетные (антисимметричные), для которых i [ Фu ] = (–1) × Фu
Если волновая функция четная, то все слагаемые, входящие в нее, также должны быть четными. Напротив, нечетная функция может состоять только из нечетных слагаемых. Это позволяет еще более упростить набор неизвестных коэффициентов, подлежащих оптимизации.
Проанализируем пространственную симметрию антисимметричных функций, найденных выше. Оператор инверсии меняет местами ядра, что выражается заменой друг на друга символов А и В в выражениях для волновых функций. (На спиновые состояния электронов и описывающие их спиновые функции a и× b оператор инверсии не влияет.) Например, для функции Ф13 найдем:
i [ Ф13 ] = i [ Аa × Вb – Вb × Аa ] =
= [ Вa × Аb – Аb × Вa ] = (– 1) Ф24
Следовательно, функции Ф13 и Ф24 не обладают необходимой пространственной симметрией, они не являются ни четными, ни нечетными. Однако, посредством процедуры симметризации из них можно построить как четную, так и нечетную комбинации.
Рассмотрим сумму:
Ф+ = Ф13 + Ф24 = Аa × Вb – Вb × Аa + Аb × Вa – Вa × Аb =
= АВ (ab + ba) – ВА (ab + ba) = [ AB – BA ](ab + ba)
Действуя оператором инверсии на пространственную часть, нетрудно определить, что она является нечетной:
i [ AB – BA ] = [ BA – AB ] = (–1)[ AB – BA ]
Теперь построим разность:
Ф– = Ф13 – Ф24 = Аa × Вb – Вb × Аa – Аb × Вa + Вa × Аb =
= АВ (ab – ba) + ВА (ab – ba) = [ AB + BA ](ab – ba)
Пространственная часть этой функции является четной:
i [ AB + BA ] = BA + AB = (+1)[ AB + BA ]
Исследуем функции Ф57 и Ф68.
Ф57 = Аa × Вa – Вa × Аa = [ АВ – BA ] (aa)
Ф68 = Аb × Вb – Вb × Аb = [ АВ – BA ] (bb)
Легко видеть, что пространственные части этих двух функций являются нечетными.
Наконец, проанализируем функции Ф9 и Ф10.
Ф9 = Аa × Аb – Аb × Аa = [ AA ] (ab – ba)
Ф10 = Вa × Вb – Вb × Вa = [ BB ] (ab – ba)
Пространственные части этих функций а переходят друг в друга при действии пространственных операций симметрии. Следовательно, их также надо подвергнуть процедуре симметризации.
Ф'+ = [ AA + BB ] (ab – ba) (четная)
Ф'– = [ AA – BB ] (ab – ba) (нечетная)
В результате получили 6 функций, обладающих как перестановочной, так и пространственной симметрией. В перестановочном отношении все они антисимметричны, а в пространственном — распадаются на два класса: четные и нечетные. Суммируем результаты в виде таблицы.
| Функ–ция | Выражение через атомные орбитали | Перестановочная симметрия | Пространственная симметрия | S | MS |
| (Ф+)u | [AB – BA] (ab + ba) | антисимм. | нечетная | ||
| (Ф–)g | [AB + BA] (ab – ba) | антисимм. | четная | ||
| Ф57 | [АВ – BA] (aa) | антисимм. | нечетная | +1 | |
| Ф68 | [АВ – BA] (bb) | антисимм. | нечетная | –1 | |
| (Ф'+)g | [AA + BB] (ab – ba) | антисимм. | четная | ||
| (Ф'–)u | [AA – BB] (ab – ba) | антисимм. | нечетная |
В последних двух столбцах указаны значения квантовых чисел — спинового (S) и магнитного спинового (MS), определяющих величину и ориентацию вектора глобального спина молекулы.
Теперь можно сконструировать три варианта глобальной волновой функции, включающих только однотипные слагаемые.
1. Четное синглетное состояние (спин S = 0)
Фg = D 1(Ф–) + D 2(Ф'+) = { D 1[ AB + BA ] + D 2[ AA + BB ]}(ab – ba)
Эта функция содержит два коэффициента (D 1 и D 2), из которых фактически только один неизвестен (условие нормировки). Пространственная часть является безузловой и электронное облако не имеет разрывов.
2. Нечетное триплетное состояние спин (S = 1)
Фu = F 1(Ф57) + F 2 (Ф+) + F 3 (Ф68) =
= [ AB – BA ] { F 1(aa) + F 2(ab + ba) + F 3(bb)}
Данная функция содержит три коэффициента (F 1, F 2 и F 3), из которых только два неизвестны. Эти коэффициенты влияют только на ориентацию суммарного вектора спина молекулы. Накладывая магнитное поле, можно сделать два из этих коэффициентов нулевыми. Пространственная форма электронного облака не зависит от ориентации спина.
3. Нечетное синглетное состояние (спин S = 0)
Ф'u = Ф'– = [ AA – BB ] (ab – ba)
В этой функции нет неизвестных коэффициентов. Пространственная часть содержит узел, и электронное облако разделено на две части.
По виду этих волновых функций можно сделать определенные выводы об энергии молекулы. Энергия (без учета магнитных взаимодействий) зависит только от пространственной части волновой функции. Поэтому у молекулы водорода должно быть три энергетических уровня и энергетическая диаграмма должна иметь следующий качественный вид:
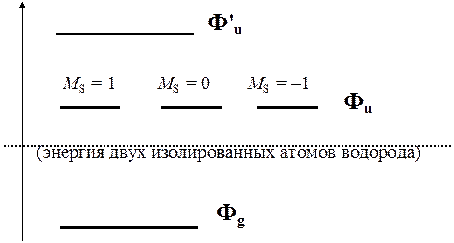
Из диаграммы видно, что два нечетных состояния физически не могут быть реализованы, так как молекула при повышении энергии распадается на отдельные атомы раньше, чем будет достигнуто какое-либо нечетное состояние. Подчеркнем существенный вывод: единственное устойчивое состояние молекулы водорода характеризуется нулевым спином (т.е. электроны в молекуле являются спаренными).
Энергетические характеристики молекулы водорода.
Располагая выражениями для волновых функций, мы можем рассчитать энергию молекулы в каждом из трех возможных состояний по стандартной формуле: Е = ò Ф* Н Ф dv. Для этого нужно знать явный вид оператора Гамильтона, который для молекулы водорода записывается в следующем виде:
Н = Н a + H b + H ab
где Н a и Н b — операторы Гамильтона для отдельных атомов водорода, содержащих электроны № 1 и № 2, соответственно.
Н a = (–h2/2 m 1)Ñ12 – e 2/ r 1a и Н b = (–h2/2 m 2)Ñ22 – e 2/ r 2b
Оператор Н ab содержит члены, характеризующие взаимодействие между атомами (энергии притяжения электронов к "чужим" ядрам (1 ® a и 2 ® b), а также энергии межэлектронного и межъядерного отталкивания) и относится сразу к обоим атомам.
Н ab = – e 2/ r 1b – e 2/ r 2а + е 2/ r 12 + e 2/ r ab
Рассмотрим для примера волновую функцию основного состояния
Ф = D 1(АВ + ВА) + D 2(AA + BB).
Вклад ионных РФ существенно меньше, чем ковалентных (D 2 << D1). Поэтому, в первом приближении, можно ограничиться учетом только ковалентных форм и взять приближенное выражение для волновой функции:
Ф» D (АВ + ВА).
Вначале найдем величину коэффициента D. Это можно сделать из условия нормировки.
òФ*Ф dv = D 2 ò (AB + BA)*(AB + BA) dv = D 2 [ ò (A*B* × AB) dv +
+ ò (A*B* × BA) dv + ò (B*A* × AB) dv + ò (B*A* × BA) dv ] = 1
В этом выражении имеется четыре интеграла. Рассмотрим первый из них. В подынтегральном выражении два сомножителя относятся к первому электрону, а два — ко второму. Такие интегралы можно представить в виде произведения более простых интегралов, каждый из которых включает только координаты только первого или только второго электрона. В результате шестимерный интеграл распадается на два трехмерных, каждый из которых представляет собой стандартное условие нормировки для атомных орбиталей. Поскольку мы принимаем атомные орбитали А и В нормированными, оба интеграла-сомножителя оказываются равными 1.
ò (A*B* × AB) dv = ò [ A*A × B*B dv a × dv b =
= òA*A dv a × òB*B dv b = 1 × 1 = 1
Проанализируем второй интеграл:
ò (A*B* × BA) dv = ò [ A* (1) B (1)× B* (2) A (2) dv 1 × dv 2 =
= òA* (1) B (1) dv 1 × òB* (2) A (2) dv 2 = S × S = S 2
Трехмерные интегралы-сомножители в этом выражении называются интегралами перекрывания (S). Величина такого интеграла определяется величиной области перекрывания, в которой обе атомные орбитали (А и В) заметно отличаются от нуля.
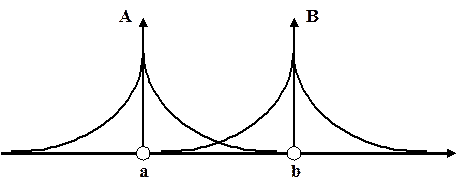
Очевидно, что S ® 0, когда ядра а и b удаляются друг от друга, и S ® 1, когда ядра сближаются.
Третий интеграл построен точно так же, как и второй, а четвертый — так же, как первый. Следовательно, выражение для нормировки приобретает вид:
òФ*Ф dv = D 2 [ 1 + S 2 + S 2 + 1] = 1
Отсюда получаем выражение для нормировочного множителя и волновой функции:
D = 1/(2 + 2 S 2)1/2 и Ф» (АВ + ВА)/(2 + 2 S 2)1/2
Подставляя это выражение в формулу для вычисления энергии, получим:
Е = ò Ф* Н Ф dv = [1/(2 + 2 S 2)] ò(АВ + ВА) * Н (АВ + ВА) dv
Раскрыв скобки в подынтегральном выражении, получим вместо одного сложного интеграла четыре более простых.
ò(АВ + ВА) * Н (АВ + ВА) dv = ò(АВ) * Н (АВ) dv + ò(АВ) * Н (ВА) dv + ò(ВА) * Н (АВ) dv + ò (ВА) * Н (ВА) dv = I + II + III + IV
Проанализируем эти четыре интеграла. Для начала можно отметить, что по структуре интегралы попарно равны друг другу(переводятся друг в друга операцией симметрии — инверсии): I = IV и II = III, и поэтому достаточно детально рассмотреть только два из них, например I и II.
Подставляя в интеграл I выражение для гамильтониана, получим сумму трех еще более простых интегралов:
ò(АВ) * Н (АВ) dv = ò(АВ) * (Н a + H b + H ab)(АВ) dv =
= ò(АВ) *(Н a)(АВ) dv + ò(АВ) *(Н b)(АВ) dv + ò(АВ) *(Н ab)(АВ) dv
Оператор Гамильтона в первом интеграл действует только на волновые функции типа А, описывающие состояние электрона № 1. Волновые функции типа В, описывающие состояние электрона № 2, для оператора Н а выступают как простые числовые множители и их можно выносить за знак оператора. Это дает возможность разбить первый из трех интегралов в произведение двух трехмерных интегралов-сомножителей:
ò(АВ) *(Н а)(АВ) dv = ò В*B dv b • ò А* (Н а) А dv a
Первый сомножитель представляет собой условие нормировки для атомной орбитали В и поэтому равен 1. Второй сомножитель представляет собой энергию электрона, принадлежащего атому водорода с ядром а, т.е. Е Нa.
Второй интеграл построен аналогично первому и равен энергии, которую имеет электрон, принадлежащий атому водорода с ядром b (Е Нb).
Третий интеграл содержит гамильтониан, описывающий оба электрона. Поэтому этот интеграл нельзя разложить в произведение двух одноэлектронных и его нужно рассматривать как меру энергии, характеризующую интенсивность взаимодействия между двумя атомами водорода. Эта энергия называется кулоновским интегралом (J ab). Ее можно представить и в более детальной записи:
ò(АВ) *(Н ab)(АВ) dv = ò(АВ) * (– e 2/ r 1b – e 2/ r 2а + е 2/ r 12 + e 2/ r ab)(АВ) dv =
= ò(АВ) * (– e 2/ r 1b)(АВ) dv + ò(АВ) * (– e 2/ r 2а)(АВ) dv +
+ ò(АВ) * (е 2/ r 12)(АВ) dv + ò(АВ) * (e 2/ r ab)(АВ) dv =
= ò(В*B) dv 2 × ò A* (– e 2/ r 1b)(А) dv 1 + ò(A*A) dv 1 × ò B* (– e 2/ r 1b)(B) dv 2 +
+ ò(АВ) * (е 2/ r 12)(АВ) dv + (e 2/ r ab)ò(А*A) dv 1 × ò(B*В) dv 2 =
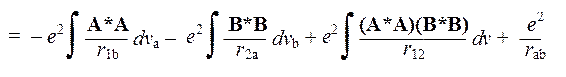
Произведение e × (A*A) dv a представляет собой электрический заряд dq a, локализованный в малом объеме dv a, принадлежащем атому На. Произведение dq a × e / r 1b, стоящее под знаком первого интеграла, — это потенциальная энергия взаимодействия заряженного объема dv a электронного облака, созданного электроном № 1 с ядром атома Нb. Поэтому первый интеграл представляет собой полную энергию кулоновского притяжения электрона № 1, расположенного на орбитали A, к ядру b; второй — энергию кулоновского притяжения электрона, расположенного на орбитали B, к ядру a; третий — энергию кулоновского отталкивания двух электронных облаков, а четвертый — энергию кулоновского отталкивания двух ядер. Кулоновский интеграл, следовательно, отражает все кулоновские взаимодействия между составными частями двух атомов, ядра которых сближены на расстояние r ab.
Таким образом, для интеграла I получаем следующую оценку:
I = Е Нa+ Е Нb+ J ab = 2 E H + J
Перейдем к анализу интеграла II. Подставляя в этот интеграл выражение для гамильтониана, получим, как и в предыдущем случае, сумму трех простых интегралов:
ò(АВ) * Н (ВА) dv = ò(АВ) * (Н a + H b + H ab)(ВА) dv =
= ò(АВ) *(Н a)(ВА) dv + ò(АВ) *(Н b)(ВА) dv + ò(АВ) *(Н ab)(ВА) dv
Первый из этих интегралов может быть разложен в произведение двух одноэлектронных:
ò(АВ) *(Н a)(ВА) dv = ò В*А dv b • ò А* (Н a) В dv a
Первый сомножитель в этом выражении представляет собой интеграл перекрывания (S). Второй сомножитель можно преобразовать, с учетом того, что гамильтониан является самосопряженным оператором, для которых выполняется правило:
ò А* Н В dv = ò В* Н * А dv
Атомная орбиталь А является собственной функцией для оператора Н a и для нее выполняется соотношение:
Н AА = Н A * А = Е На × А
Следовательно,
ò А* (Н a) В dv a = ò В* Н a * А dv a = ò В* Е На А dv a =
= Е На × ò В*А dv 1a = Е На × S
С учетом первого множителя получаем величину Е На × S 2.
Второй интеграл устроен аналогично первому и поэтому равен Е Нb × S 2.
Третий интеграл не поддается разложению на одноэлектронные сомножители и должен рассматриваться как глобальная характеристика молекулы, точнее как характеристика межатомного взаимодействия. Этот интеграл называется обменным (K). Его, как и кулоновский, можно представить в более детальной записи:
ò(АВ) *(Н ab)(ВA) dv = ò(АВ) * (– e 2/ r 1b – e 2/ r 2а + е 2/ r 12 + e 2/ r ab)(ВA) dv =
= ò(АВ) * (– e 2/ r 1b)(ВA) dv + ò(АВ) * (– e 2/ r 2а)(ВA) dv +
+ ò(АВ) * (е 2/ r 12)(ВA) dv + ò(АВ) * (e 2/ r ab)(ВA) dv =
= ò(В*A) dv 2 × ò A* (– e 2/ r 1b)(B) dv 1 + ò(A*B) dv 1 × ò B* (– e 2/ r 1b)(A) dv 2 +
+ ò(АВ) * (е 2/ r 12)(ВA) dv + (e 2/ r ab)ò(А*B) dv 1 × ò(B*A) dv 2 =
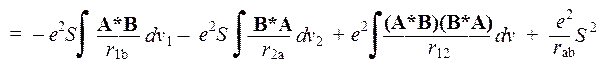
Из формы интегралов в этом выражении видно, что они представляют собой особые кулоновские поправки к полной энергии молекулы. Они возникают вследствие того, что в области перекрывания плотность электронного облака молекулы не равна сумме плотностей двух исходных атомных электронных облаков. К этой сумме добавляется интерференционный вклад. Другими словами, в области перекрывания возникает дополнительный электрический заряд, величина которого в малом объеме dv равна eS (A*B) dv 1 = eS (В*А) dv 2. Этот дополнительный заряд взаимодействует, с одной стороны, с обеими ядрами, а с другой стороны — его части взаимодействуют между собой (уплотнение электронного облака в межъядерном пространстве приводит к повышению потенциальной кулоновской энергии).
Можно сказать, что кулоновский интеграл (J) вычисляется в предположении, что в сферически симметричные электронные облака атомов (А и В) при их вхождению в состав молекулы не изменились. В действительности, в следствие интерференции в области перекрывания, оба эти облака деформировались: А ® А' и B ® B'. В результате энергия межатомных кулоновских взаимодействий была вычислена неправильно. Обменный интеграл представляет собой необходимую поправку.
В итоге получаем следующую оценку интеграла II:
II = Е На × s 2 + Е Нb × s2 + K = 2 E H × s 2 + K
Теперь, с учетом равенств I = IV и II = III, запишем полное выражение для энергии молекулы:
Eg = (I + II + III + IV)/(2 + 2 s 2) = (2 E H + J + 2 E H × s 2 + K +
+ 2 E H × s 2 + K + 2 E H + J)/(2 + 2 s 2) =
= [4 E H (1 + s 2) + 2 (J + K)]/2(1 + s2) = 2 E H + (J + K)/(1 + s2)
Таким образом, энергия молекулы водорода представлена в виде суммы двух вкладов:
1) энергии двух атомов, из которых молекула образовалась, и
2) энергетической поправки на межатомные взаимодействия.
Из формулы видно, что эта поправка состоит из двух частей — кулоновской и обменной. Их величины можно вычислить, зная явный вид атомных орбиталей А и В.
Подчеркнем, что найденное выражение для энергии носит общий характер в методе ВС. Независимо от размера молекулы, энергия всегда представляется в виде суммы энергий изолированных атомов, из которых молекула образована, и поправок (кулоновских и обменных) на межатомные взаимодействия.
Аналогичные вычисления можно выполнить и для других состояний. Например, для триплетного возбужденного состояния с волновой функцией Фu получим:
Eu = 2 E H + (J – K)/(1 – s 2)
Следует подчеркнуть, что значение обменного интеграла отрицательно. Поэтому энергия триплетного состояния выше, чем основного (Eu > Eg).
Дата добавления: 2015-07-20; просмотров: 64 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Перестановочная симметрия волновой функции | | | Влияние межъядерного расстояния |