Построение базисного набора. Электронное строение молекул

ЭЛЕКТРОННОЕ СТРОЕНИЕ МОЛЕКУЛ

МОЛЕКУЛА ВОДОРОДА

При описании электронной структуры молекул основная задача сводится к построению глобальной волновой функции электронной оболочки. Для решения этой задачи наиболее часто употребляются два подхода:

– метод ВС (валентных схем),

– метод МО (молекулярных орбиталей).

Основные идеи и особенности этих методов можно проследить на примере простейшей молекулы водорода.

Метод ВС

Метод ВС основан на принципе суперпозиции (т.е. на возможности представить вектор состояния или волновую функцию в виде линейной комбинации других векторов или функций, которые являются в определенных отношениях более простыми. Например, для волновой функции ЛК будет иметь такой общий вид:

Ф = å (С_i • Ф _i) = С₁ • Ф₁ + С₂ • Ф ₂ +.... + С_n • Ф _n

где Ф _i — базисные функции, а С_i — коэффициенты ЛК.

Подчеркнем тот факт, что как Ф, так и Ф _i имеют глобальный характер и относятся ко всей молекуле в целом.

Теперь остается решить две проблемы. Первая заключается в выборе удобных базисных функций, а вторая — в установлении численных значений коэффициентов ЛК.

Построение базисного набора

Очевидно, что явный вид базисных волновых функций (Ф _i) должен быть известен, иначе сама идея суперпозиционного разложения теряет смысл. В квантовой механике глобальная волновая функция известна только тогда, когда система состоит из невзаимодействующих частиц. Отсюда сразу находим, что базисные волновые функции описывают такие состояния молекулы, когда она "разрезана" на отдельные части, причем такие, что их локальные (одночастичные) волновые функции известны. В методе ВС в качестве таких частей молекулы выбираются т.н. "атомы".Под атомами понимаются одноядерные подсистемы, которые могут включать в себя любое число электронов.

Всякий базисный набор в квантовой механике задается посредством некоторого прибора — спектрального анализатора. В данном случае этот прибор может иметь следующий принцип действия. В реальной молекуле "атомы" перекрываются в том смысле, что для конкретного электрона невозможно указать к какому именно атому он принадлежит. Прибор представляет собой совокупность перегородок, непроницаемых для электронов и разделяющих молекулу на не перекрывающиеся между собой отсеки. После "измерения", т.е. введения перегородок в молекулу, внутри каждого отсека окажется одно атомное ядро и несколько электронов. Благодаря влиянию ядра эти электроны будут двигаться внутри отсека почти так же, как в изолированном атоме.

Можно сказать, что наш прибор предназначен для измерения особой наблюдаемой — принадлежности электрона тому или иному "атому" в составе молекулы. Пока межатомных перегородок нет (до измерения), невозможно ответить на вопрос: к какому атому принадлежит i -ый электрон?. Напротив, после введения перегородок (после измерения) на любой подобный вопрос можно дать точно определенный ответ: i -ый электрон принадлежит j -ому "атому".

Как и во всех других случаях применения спектрального анализатора, результат конкретного измерения (т.е. попадание конкретного электрона в конкретный отсек-"атом") случаен. Поэтому мы должны рассмотреть все возможные варианты распределения электронов по отсекам прибора. Каждый конкретный способ распределения приводит к определенной резонансной форме (РФ), которая представляет собой молекулу, находящуюся в особом состоянии. Переход в это особое состояние вызван введением межатомных перегородок (измерением). Превращение молекулы в одну из ее РФ приводит к преобразованию волновой функции молекулы в волновую функцию РФ.

Волновые функции резонансных форм (Ф₁, Ф₂, …, Ф _n) и образуют базисный набор для анализа волновой функции реальной молекулы (Ф).

Ф = å (С_i • Ф _i) = С₁ • Ф₁ + С₂ • Ф ₂ +.... + С_n • Ф _n

Таким образом, базисный набор метода ВС можно определить с помощью спектрального анализатора, в котором молекула разделяется перегородками на "атомы". В каждой резонансной форме имеется совокупность "атомов", разделенных перегородками, что позволяет считать их невзаимодействующими. Поэтому волновая функция резонансной формы может быть построена в виде простого произведения волновых функций составляющих ее "атомов":

Ф _i = Y₁ • Y₂ •.... • Y _i •... • Y _n

где Y _i — волновая функция i –го "атома", которая строится по стандартным правилам на основе теории МЭА (в виде определителя Слэтера).

Перейдем к рассмотрению конкретного объекта — молекулы водорода. Ввиду того, что эта молекула содержит всего два ядра, наш прибор будет устроен чрезвычайно просто — он содержит всего одну перегородку, разделяющую молекулу на две одноядерных подсистемы ("атома"):

Первый этап описания заключается в перечислении всех возможных исходов такого разрезания молекулы в отношении способа распределения электронов по двум отсекам.

При этом мы должны учесть не только сам факт попадания электрона в конкретный "атом", но и его состояние — характер пространственного и спинового движения, выражающийся двумя сомножителями волновой функции (АСО). Можно также полагать, что в результате процедуры разрезания образующиеся атомы водорода могут получатся не только в основном (1s), но и в одном из возбужденных состояний (2s, 2p и т.д.), причем каждая такая АО может иметь в качестве спинового множителя либо a-, либо b-функцию. В идеале все возможные варианты должны быть учтены. Ясно, однако, что этот идеал недостижим, так как число возможных вариантов бесконечно велико. На практике мы должны использовать ограниченный базис, включающий только такие исходы, вероятность которых достаточно велика. Правило, согласно которому осуществляется отбор, сводится к следующему:

вероятность реализации некоторой резонансной формы тем больше, чем меньше ее энергия.

Поэтому в первом приближении мы можем полагать, что атомы, составляющие резонансные формы, могут находиться только в основном электронном состоянии 1s. Тогда у каждого электрона возможны всего две АСО: (1s×a) и (1s×b). При этом пространственная часть АСО будет центрирована либо на ядре H_a, либо на ядре H_b. Для упрощения записи обозначим эти пространственные части буквами А и В соответственно. Теперь легко перечислить все допустимые исходы разрезания молекулы водорода на два "атома" — резонансные формы. Для удобства разобьем их на группы.

Синглетные РФ ковалентного типа (суммарный спин S = 0)

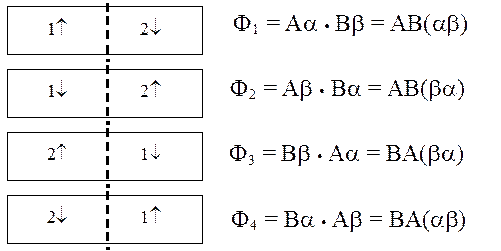
Триплетные РФ ковалентного типа (суммарный спин S = 1)

---

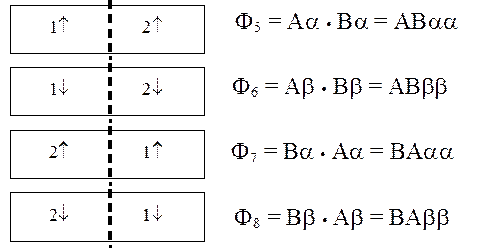
Дата добавления: 2015-07-20