
Читайте также:
|
| 1 порядку | 2 порядку |
Точка х0 - якщо не виконується хоча б одна з умов 1, 4, 5.
Якщо лівостороння границя функції і правостороння існують, але не рівні між собою 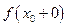  
 х
Стрибок функції: х
Стрибок функції: 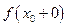 - -  або або  - -  - усувний стрибокякщо стрибок дорівнює нулю. Якщо - усувний стрибокякщо стрибок дорівнює нулю. Якщо  не існує. Якщо не існує. Якщо  існує, то це ізольована точка. існує, то це ізольована точка.
|
Точка х0 – якщо не існує або нескінчена хоча б одна з границь функції зліва або справа у точці х0.
Неусувний розрив (нескінчений).
 0 а х 0 а х
|
Правила відшукання точок розриву:
| Елементарна функціяможе мати розрив, якщо: 1. Тільки в окремих точках, але не може бути розривною у всіх точках будь-якого інтервалу. 2. Тільки в точках, де вона не визначена, якщо вона визначена хоча б з однієї сторони від цієї точки в скіль завгодно близьких до неї точках. |
| Неелементарна функціяможе мати розриви, як в точках, де вона не визначена, так і в точках, де вона визначена. |
| Якщо функція задана декількома різними формулами для різних інтервалів змінення х, то вона може мати розриви саме в точках, де змінюється її аналітичний вираз. |
Дата добавления: 2015-07-25; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Точки розриву функції | | | Опитувальні листи до лекцій |