
Читайте также:
|
Заповнити опитувальні листи в колонці „Код відповіді”.
Модуль №1. Елементи лінійної алгебри
| № | Питання | Код відповіді |
| 1. | Визначники – це: a) Число у вигляді довільної таблиці числових або літерних значень. b) Число у вигляді квадратної таблиці числових або літерних значень. c) Прямокутна таблиця числових або літерних значень. | |
| 2. | Детермінант позначається:
a) А, В,...
b)  ,
c) ,
c)  d)
d)  , ( , ( ) )
| |
| 3. | Матриці – це: a) Число у вигляді довільної таблиці числових або літерних значень. b) Число у вигляді прямокутної таблиці. c) Довільна таблиця числових або літерних значень. d) Квадратна таблиця, яку можна обчислити. | |
| 4. | Матриці позначаються:
a) А, В,...,  b)
b)  , , 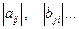 c)
c)  d)
d)  , , 
| |
| 5. | Добуток прямокутних матриць існує:
a) завжди.
b)  , коли , коли  c)
c)  , коли , коли 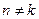 d)
d)  , коли , коли 
| |
| 6. | Для знаходження оберненої матриці застосовують:
a) Алгебраічні доповнення елементів прямокутної матриці, 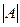 та операцію транспонування.
b) Алгебраічні доповнення елементів квадратної
матриці, та операцію транспонування.
b) Алгебраічні доповнення елементів квадратної
матриці,  та операцію транспонування.
c) Мінори елементів квадратної матриці, та операцію транспонування.
c) Мінори елементів квадратної матриці, 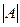 та операцію множення матриць.
d) Мінори елементів будь-якої матриці, та операцію множення матриць.
d) Мінори елементів будь-якої матриці, 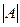 та операцію піднесення матриці у степень. та операцію піднесення матриці у степень.
| |
| 7. | Ранг матриці – це... a) Порядок будь-якого ненульового мінору. b) Порядок найвищого ненульового мінору. c) Порядок найвищого нульового мінору. d) Будь-який визначник із елементів матриці. | |
| 8. | Система лінійних алгебраічних рівнянь - це... a) Сукупність будь-якої кількості рівнянь. b) Сукупність нескінченої кількості будь-яких рівнянь c) Сукупність скінченої кількості лінійних рівнянь. d) Сукупність однорідних рівнянь. | |
| 9. | Теорема Кронекера –Капелі: „Для сумісної системи лінійних рівнянь необхідно і достатньо...
a)   , де А – матриця, А* - розширена матриця
b) , де А – матриця, А* - розширена матриця
b)  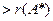 , де А* – матриця, А - розширена матриця
c) , де А* – матриця, А - розширена матриця
c)   , де А – матриця, А* - розширена матриця
d) , де А – матриця, А* - розширена матриця
d)   , де А* – матриця, А - розширена матриця , де А* – матриця, А - розширена матриця
| |
| Необхідність мати однакову кількість рівнянь і змінних a) Для метода Гауса і метода оберненої матриці. b) Для метода Крамера і метода оберненої матриці. c) Для метода оберненої матриці і правила Крамера. | ||
| Сутність метода Гауса полягає в... a) Складанні і обчисленні визначників. b) В розв’язанні матричного рівняння. c) Метод послідовного виключення невідомих. d) В знаходженні оберненої матриці. | ||
| Сутність метода Крамера полягає в... a) Складанні і обчисленні визначників. b) В розв’язанні матричного рівняння. c) Метод послідовного виключення невідомих. d) В знаходженні оберненої матриці. |
Модуль №2. Аналітична геометрія.
| № | Питання | Код відповіді |
| 1. | Вектор – це... a) Величина скалярна (характеризується модулем). b) Величина, яка характеризується числовим значенням і напрямком. c) Відрізок, довжина якого дорівнює одиниці. | |
| 2. | Скалярний добуток векторів застосовується для... a) Визначення кута між прямими та площинами. b) Обчислення площі паралелограма. c) Обчислення об’єму паралелепіпеда. | |
| 3. | Векторний добуток векторів застосовується для... a) Визначення кута між прямими та площинами. b) Обчислення площі паралелограма. с) Обчислення об’єму паралелепіпеда. | |
| 4. | Змішаний добуток векторів застосовується для... c) Визначення кута між прямими та площинами. d) Обчислення площі паралелограма. с) Обчислення об’єму паралелепіпеда. | |
| 5. | Пряма на площині визначається...
a) Точкою та напрямком (нормальним вектором  (а,b) або (а,b) або  (m,n) напрамляючим вектором).
b) Точкою та напрямком (нормальним вектором).
c) Точкою та напрямком (напрамляючим вектором). (m,n) напрамляючим вектором).
b) Точкою та напрямком (нормальним вектором).
c) Точкою та напрямком (напрамляючим вектором).
| |
| 6. | Пряма в просторі визначається...
a) Точкою та напрямком (нормальним вектором  (а,b) або (а,b) або  (m,n) напрамляючим вектором).
b) Точкою та напрямком (нормальним вектором).
с) Точкою та напрямком (напрамляючим вектором). (m,n) напрамляючим вектором).
b) Точкою та напрямком (нормальним вектором).
с) Точкою та напрямком (напрамляючим вектором).
| |
| 7. | Площина в просторі визначається...
a) Точкою та напрямком (нормальним вектором  (а,b) або (а,b) або  (m,n) напрамляючим вектором).
b) Точкою та напрямком (нормальним вектором).
С) Точкою та напрямком (напрамляючим вектором). (m,n) напрамляючим вектором).
b) Точкою та напрямком (нормальним вектором).
С) Точкою та напрямком (напрамляючим вектором).
| |
| 8. |  = 0 визначає...
a) Рівняння прямої у просторі.
b) Рівняння площини, що проходе через 3 точки.
c) Канонічне рівняння прямої.
d) Загальне рівняння площини. = 0 визначає...
a) Рівняння прямої у просторі.
b) Рівняння площини, що проходе через 3 точки.
c) Канонічне рівняння прямої.
d) Загальне рівняння площини.
| |
| 9. | Умова паралельності прямих у просторі:
a)  .
b) .
b)  c)
c)  .
d) .
d)  . .
| |
Умова перпендикулярності площин:
a)  .
b) .
b)  .
c) .
c)  .
d) .
d)  . .
| ||
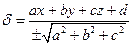 -це формула...
a) Відстані від точки до прямої на площині.
b) Відстані від точки до площини.
c) Відхилення від точки до прямої у просторі.
d) Відхилення від точки до площини. -це формула...
a) Відстані від точки до прямої на площині.
b) Відстані від точки до площини.
c) Відхилення від точки до прямої у просторі.
d) Відхилення від точки до площини.
| ||
 Це малюнок...
a) Еліпса Це малюнок...
a) Еліпса  b) Гіперболи у2 = 2рх
c) Параболи х2 = 2ру
d) Кола
b) Гіперболи у2 = 2рх
c) Параболи х2 = 2ру
d) Кола 
| ||
Поверхнєю 2 порядку є рівняння:
a) Ах + Ву + Сz + D = 0
b)  с) Ах2 + Ву2 + Сх + Dу + F = 0
c)
с) Ах2 + Ву2 + Сх + Dу + F = 0
c) 
|
Модуль №3. Вступ до математичного аналізу.
| № | Питання | Код відповіді |
| 1. |  Це малюнок...
a) Перетину множин.
b) Об’єднання множин.
c) Різниці множин.
d) Доповнення множин. Це малюнок...
a) Перетину множин.
b) Об’єднання множин.
c) Різниці множин.
d) Доповнення множин.
| |
| 2. | Функція - це... a) Фігура в просторі. b) Дія алгебоаічна. c) Закон про відповідність. d) Перетворення простору. | |
| 3. | Обмеженням для області визначення є:
a) Відшукання 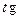 для аргументів для аргументів 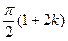 , ,  .
b) Логарифмування недодатніх чисел.
c) Добування коренів непарних степенів з від’ємних чисел.
d) Відшукання .
b) Логарифмування недодатніх чисел.
c) Добування коренів непарних степенів з від’ємних чисел.
d) Відшукання  для аргументів для аргументів  f f  1. 1.
| |
| 4. | Складна функція – це... a) Трансцендентна функція. b) Елементарна функція. c) Іраціональна функція. d) Композиція функцій. | |
| 5. | Монотонність функції – це... a) Екстремуми функції. b) Обмеженість функції. c) Зростання, спадання функції. d) Періодичність функції. | |
| 6. | Яка з формул є чудовою границею?
a)  .
b) .
b)  .
c) .
c) 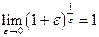 .
d) .
d)  = е. = е.
| |
| 7. | Яка з формул належить до основних еквівалентностей?
a) 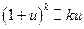 .
b) .
b)  -1
c) -1
c)  .
d) .
d) 
| |
| 8. | Дозволяє позбавитися від невизначеностей теорема... a) Теорема Безу. b) Теорема Гауса. c) Теорема Вейєрштраса. d) Теорема Даламбера. | |
| 9. | Функція  неперервна в точці х0, якщо вона...
a) Не визначена в точці х0 і в деякому її колі та існує значення неперервна в точці х0, якщо вона...
a) Не визначена в точці х0 і в деякому її колі та існує значення  та існує границя та існує границя  .
b) Визначена в точці х0 і в деякому її колі та існує значення .
b) Визначена в точці х0 і в деякому її колі та існує значення  та існує границя та існує границя  = =  .
c) Визначена в точці х0 і не існує границя .
c) Визначена в точці х0 і не існує границя 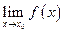 . .
| |
| Точка розриву першого роду – це... a) Коли односторонні границі існують і однакові. b) Коли односторонні границі існують, але різні. c) Коли хоча б одна з односторонніх границь – не існує або нескінчена. d) Коли одна з односторонніх границь – нескінчена. | ||
| Точка розриву другого роду – це... a) Коли односторонні границі існують, але різні. b) Коли хоча б одна з односторонніх границь – не існує або нескінчена.. с) Коли односторонні границі існують і однакові. | ||
Стрибок функції дорівнює...
a)  + +  .
b) .
b)  · ·  .
c) .
c)  - -  . .
|
Дата добавления: 2015-07-25; просмотров: 43 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Класифікація точок розриву | | | Практичні заняття |