Означення
1.Функція  неперервна в точці х0, якщо вона:
1) Визначена в точці х0 і в деякому її колі та існує значення неперервна в точці х0, якщо вона:
1) Визначена в точці х0 і в деякому її колі та існує значення  .
2) Існує границя .
2) Існує границя  , незалежно від способу прямування їх до х0.
3) А = , незалежно від способу прямування їх до х0.
3) А =  .
2.Функція у = .
2.Функція у =  неперервна в точці х0, якщо вона визначена в точці х0 і в деякому її колі та нескінчено малому прирості аргументу неперервна в точці х0, якщо вона визначена в точці х0 і в деякому її колі та нескінчено малому прирості аргументу 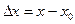 відповідає нескінчено малий приріст функції такий, що відповідає нескінчено малий приріст функції такий, що  , де ∆у – приріст функції являє собою нескінчено малу величину від ∆х.
3.Функція у = , де ∆у – приріст функції являє собою нескінчено малу величину від ∆х.
3.Функція у =  неперервна на інтервалі (а,в), якщо вона неперервна в кожній точці цього інтервалу.
4. Конструктивне визначення (необхідна і достатня умова неперервності функції):
Функція у = неперервна на інтервалі (а,в), якщо вона неперервна в кожній точці цього інтервалу.
4. Конструктивне визначення (необхідна і достатня умова неперервності функції):
Функція у =  неперервна в точці х0, якщо виконуються 5 умов:
1) Існує неперервна в точці х0, якщо виконуються 5 умов:
1) Існує  . Якщо . Якщо  визначена в визначена в 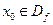 і в її околі.
2) Існує ліва границя функції в точці х0. і в її околі.
2) Існує ліва границя функції в точці х0.  .
3) Існує права границя функції в точці х0. .
3) Існує права границя функції в точці х0. 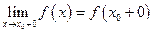 .
4) Виконується рівність .
4) Виконується рівність  = = 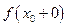 = а.
5) Виконується рівність = а.
5) Виконується рівність  = а.
Функція розривна в точці = а.
Функція розривна в точці  , якщо вона визначена в скіль завгодно близьких точках, але не в точці , якщо вона визначена в скіль завгодно близьких точках, але не в точці  , тобто коли хоча б одна з умов не виконується. , тобто коли хоча б одна з умов не виконується.
|

 неперервна в точці х0, якщо вона:
1) Визначена в точці х0 і в деякому її колі та існує значення
неперервна в точці х0, якщо вона:
1) Визначена в точці х0 і в деякому її колі та існує значення  .
2) Існує границя
.
2) Існує границя  , незалежно від способу прямування їх до х0.
3) А =
, незалежно від способу прямування їх до х0.
3) А =  .
2.Функція у =
.
2.Функція у =  неперервна в точці х0, якщо вона визначена в точці х0 і в деякому її колі та нескінчено малому прирості аргументу
неперервна в точці х0, якщо вона визначена в точці х0 і в деякому її колі та нескінчено малому прирості аргументу 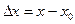 відповідає нескінчено малий приріст функції такий, що
відповідає нескінчено малий приріст функції такий, що  , де ∆у – приріст функції являє собою нескінчено малу величину від ∆х.
3.Функція у =
, де ∆у – приріст функції являє собою нескінчено малу величину від ∆х.
3.Функція у =  неперервна на інтервалі (а,в), якщо вона неперервна в кожній точці цього інтервалу.
4. Конструктивне визначення (необхідна і достатня умова неперервності функції):
Функція у =
неперервна на інтервалі (а,в), якщо вона неперервна в кожній точці цього інтервалу.
4. Конструктивне визначення (необхідна і достатня умова неперервності функції):
Функція у =  неперервна в точці х0, якщо виконуються 5 умов:
1) Існує
неперервна в точці х0, якщо виконуються 5 умов:
1) Існує  . Якщо
. Якщо  визначена в
визначена в 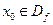 і в її околі.
2) Існує ліва границя функції в точці х0.
і в її околі.
2) Існує ліва границя функції в точці х0.  .
3) Існує права границя функції в точці х0.
.
3) Існує права границя функції в точці х0. 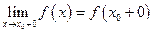 .
4) Виконується рівність
.
4) Виконується рівність  =
= 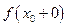 = а.
5) Виконується рівність
= а.
5) Виконується рівність  = а.
Функція розривна в точці
= а.
Функція розривна в точці  , якщо вона визначена в скіль завгодно близьких точках, але не в точці
, якщо вона визначена в скіль завгодно близьких точках, але не в точці  , тобто коли хоча б одна з умов не виконується.
, тобто коли хоча б одна з умов не виконується.