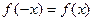Парність.

- парна, графік симетричний відносно вісі ОУ, де ,

- непарна, графік симетричний відносно початку координат.

- загального вигляду (не парна ні непарна).

5. Періодичність.

Функція f, визначена на множині А періодична на А, якщо існує число Т таке, що х + Т 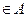, та f (х + Т) , , Т – період функції (найменше додатнє число).

Властивості:

1. Якщо Т – період функції f, то число - теж період функції f.

2. Якщо функція у = f(х) періодична з періодом Т, функція у = Аf(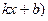 - теж періодична з періодом , де А, - постійні числа.

3. Композиція двох періодичних функцій - функція періодична з періодом Т

4. Для побудови графіка періодичної функції з періодом Т, достатньо побудувати урафік на відрізку довжиною Т і паралельно перенести його вздовж вісі ОХ на відстань лівворуч та праворуч.

Дата добавления: 2015-07-25