
Читайте также:
|
1. Елементарні функції- функції, отримані з основних елементарних
функцій за допомогою скінченого числа алгебраічних операцій (додавання, віднімання, множення, ділення) і суперпозиції функцій (взяття функції від функції).
1) Степенева  , де n – дійсне число.
2) Показникова , де n – дійсне число.
2) Показникова  , де , де  .
3) Експоненціальна .
3) Експоненціальна  , де , де  2,7182.
4) Логарифмічна 2,7182.
4) Логарифмічна  , де , де  . (Натуральна . (Натуральна  )
5) Тригонометричні: )
5) Тригонометричні:  , ,  , ,  , ,  , ,  .
6) Обернені тригонометричні: .
6) Обернені тригонометричні:
 , ,  , ,  .
7) Гіперболічні: .
7) Гіперболічні:  , ,  , , , ,  2. Алгебраічні функції -мають 4 арифметичні операції.
1) Ціла раціональна функція –многочлен n степені.
2. Алгебраічні функції -мають 4 арифметичні операції.
1) Ціла раціональна функція –многочлен n степені.
 , де , де  - дійсні числа, - дійсні числа, 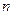 - ціле.
Степень многочлена визначається найвищою степенню його одночленів.
Корень многочлена – таке значення змінного ч, при якому многочлен перетворюється в нуль Р(х) = 0.
Приведенним є многочлен - ціле.
Степень многочлена визначається найвищою степенню його одночленів.
Корень многочлена – таке значення змінного ч, при якому многочлен перетворюється в нуль Р(х) = 0.
Приведенним є многочлен 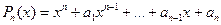 , коли , коли  .
Теорема Даламбера, уточнив Гаус – доводе існування кореня у многочлена, не даючи методів знаходження його.
Теорема Безу: Якщо число .
Теорема Даламбера, уточнив Гаус – доводе існування кореня у многочлена, не даючи методів знаходження його.
Теорема Безу: Якщо число  - корень многочлена Р(х), то цей многочлен без залишку ділиться на (х – а) і навпаки. - корень многочлена Р(х), то цей многочлен без залишку ділиться на (х – а) і навпаки.  .
Якщо серед коренів є рівні, то вони кратні: .
Якщо серед коренів є рівні, то вони кратні: 
 2) Дробово-раціональна функція.
2) Дробово-раціональна функція.
 , де , де 
 - дійсні многочлени.
Правильна дріб – якщо степень чисельника нище степеня знаменника.
Частинні випадки: 1. Дробово – лінійна - дійсні многочлени.
Правильна дріб – якщо степень чисельника нище степеня знаменника.
Частинні випадки: 1. Дробово – лінійна  2. Обернена пропорційність
2. Обернена пропорційність  .
3) Іраціональна функція –алгебраічна функція з добування кореня n
степеня. .
3) Іраціональна функція –алгебраічна функція з добування кореня n
степеня.
 , тригонометричні та обеонені тригонометричні. , тригонометричні та обеонені тригонометричні.

|
Характеристики функцій:
Функція f(х), визначена в точці х = х0 та в її околі неперервна при х = х0., якщо нескінчено малому приросту аргументу ∆х в точці х = х0 відповідає нескінчено малий приріст ∆у.
Якщо функція f(х) неперервна в кожній точці інтервалу (а,b), то вона неперервна в інтервалі (а,b).
Функція f(х) неперервна на відрізку [а,b], якщо вона неперервна в інтервалі (а,b) і на кінцях інтервалу, зліва і справа.
Властивості неперервних функцій: 1. Алгебраічна сума та добуток скінченої кількості функцій, неперервних в точці х0, є функцією неперервною в х0. 2. Частка скінченої кількості функцій, неперервних в точці х0, є функцією неперервною в х0, якщо дільник при х = х0 не дорівнює нулю. 3. Неперервна функція від неперервної функції є також функцією неперервною. 4. Усі основні елементарні функції неперервні в кожній точці своєї 5. Будь-яка елементарна функція неперервна в кожній точці своєї 6. Функція, обернена до неперервної функції – неперервна на цьому інтервалі. Теорема Вейєрштраса. Якщо функція f(х) неперервна на відрізку [а,b], то вона обмежена на відрізку [а,b], тобто існують числа М і m, що Дата добавления: 2015-07-25; просмотров: 47 | Нарушение авторских прав
|