
|
Читайте также: |
1. Якщо послідовність має границю, то ця границя єдина.
2. Послідовність, що має границю є обмеженою.
3. Теорема Вейєрштраса (існування границі монотонної обмеженої послідовності):
1) Якщо послідовность  не спадає і обмежена зверху не спадає і обмежена зверху  .
2) Якщо послідовность .
2) Якщо послідовность  не зростає і обмежена знизу не зростає і обмежена знизу  4. Якщо послідовность
4. Якщо послідовность  має границю має границю  та послідовність та послідовність  має границю має границю  , то:
1) , то:
1)  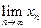 + + 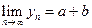 .
2) .
2)  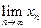 ∙ ∙ 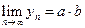 .
3) .
3) 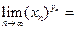  4)
4) 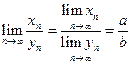 .
5. Якщо .
5. Якщо    , то , то  .
6. Якщо існує послідовність .
6. Якщо існує послідовність 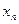   , де , де  та та  , то , то  . .
|
Дата добавления: 2015-07-25; просмотров: 74 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Означення границі | | | Нескінченно малі та нескінченно великі |