Метод Зейделя. Метод Зейделя отличается от метода Якоби тем, что вычисления ведутся не по формулам

Метод Зейделя отличается от метода Якоби тем, что вычисления ведутся не по формулам (3.4), а по следующим формулам:

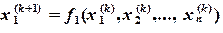
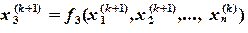(3.6)

…

При решении систем нелинейных уравнений необходимо определить приемлемое начальное приближение. Для случая двух уравнений с двумя неизвестными начальное приближение находится графически.

Сходимость метода Зейделя (Якоби тоже) зависит от вида функции в (3.2), вернее она зависит от матрицы, составленной из частных производных:

, (3.7)

где .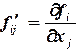

Итерационный процесс сходится, если сумма модулей каждой строки 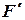меньше единицы в некоторой окрестности корня:

,

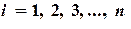
или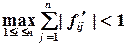

Пример 3.1. Найти решение системы методом Зейделя с точностью :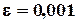

(3.8)

Решение: Представим (3.8) в виде (3.5):

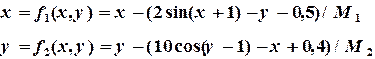(3.9)

Задаем начальные приближения , .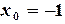

Запишем достаточное условие сходимости и определяем , :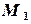

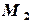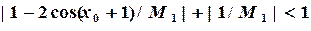
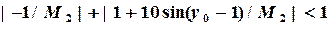
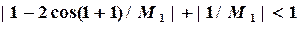
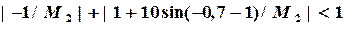
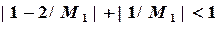и

Определяем частныезначения , ,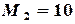которые удовлетворяют неравенствам

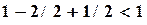и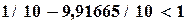

Переходим к реализации итерационного процесса:

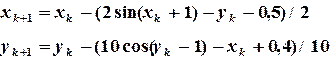
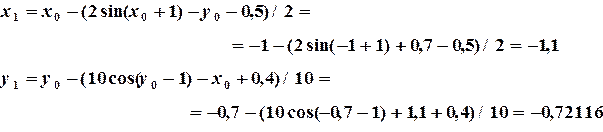
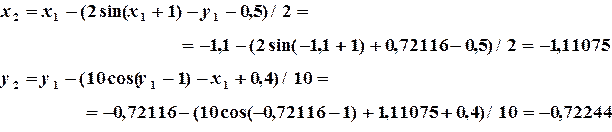
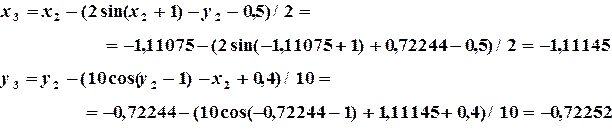
Определяем погрешностьпо формуле :

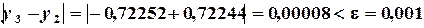
Таким образом, имеем решение: , .

Программа, реализующая решение данной задачи, представлена на рис. 3.1.

CLS

INPUT X,Y, M1,M2

1 X=X-(2*SIN(X+1)-Y - 0.5)/M1

Y=Y-(10*COS(Y-1)-X+0.4)/M2

PRINT X,Y

INPUT TT

GOTO 1

END

Рис. 3.1. Программа решения системы нелинейных уравнений методом Зейделя.

Дата добавления: 2015-07-25