Метод простой итерации (метод Якоби).

Суть вычислений итерационными методами состоит в следующем: расчет начинается с некоторого заранее выбранного приближения (начального приближения). Вычислительный процесс, использующий матрицу 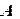, вектор системы (2.1) и , приводит к новому вектору :

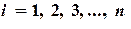, (2.11)

Затем процесс повторяется, только вместо используется новое значение . На 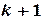-м шаге итерационного процесса по получают:

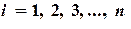, (2.12)

При выполнении некоторых заранее оговоренных условий процесс сходится при . Сходимость метода простой итерации обеспечивается при выполнении условия преобладания диагональных элементов матрицы A, т.е. при:

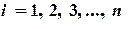, (2.13)

Заданная точность достигается при выполнении условия:

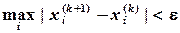(2.14)

Пример 2.5. Преобразовать систему уравнений:

(2.15)

к виду, пригодному для построения итерационного процесса методом Якоби и выполнить три итерации.

Решение. Достаточное условие сходимости (2.13) выполняется, поэтому начальное приближение может быть любым.

В -ом уравнении все члены, кроме 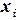, переносятся в правую часть:

(2.16)

Задается начальное приближение , которое подставляется в правую часть. Обычно , , и получают результаты первой итерации:

Результаты первой итерации подставляют в правую часть и получают результаты второй итерации:

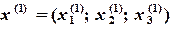Результаты второй итерации подставляют в правую часть и получают результаты третьей итерации:

Определяют достигнутую точность

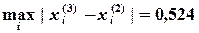
Пример 2.6. Решить систему уравнений методом Якоби с помощью программы Excel с точностью :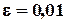

Дата добавления: 2015-07-25