Порядок решения.

1) Представить систему в виде (2.16);

2) Ввести в ячейки A1:G1, D2:G2 заголовки столбцов (рис. 2.4);

3) В ячейки A2:C2 – начальное приближение 0, 0, 0;

4) В ячейку A3 – формулу 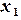=(7-4*B2+C2)/7

5) В ячейку B3 – формулу 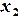=(-2-2*A2-3*C2)/6

6) В ячейку C3 – формулу 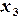=(4+A2-B2)/4

7) В ячейку D3 – формулу погрешности 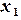=ABS(A3-A2)

8) Выделить ячейку D3 и скопировать формулу в соседние ячейки E3:F3 при помощи маркера заполнения;

9) В ячейку G3 – формулу максимальной погрешности =МАКС(D3:F3)

10) Выделить ячейки A3:G3 и скопировать формулы в соседние ячейки расположенных ниже строк A4:G4, A5:G5 и т.д.при помощи маркера заполнения. Каждая новая строка содержит результаты очередного приближения;

11) Ячейки A15, B15, C15 содержат решение системы уравнений, соответствующее заданной точности (G15).

Приближенное решение системы с точностью :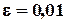

, ,

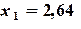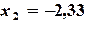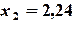
	A	B	C	D	E	F	G
	x1	x2	x3	погрешности
				x1	x2	x3	max
		-0,333			0,3333
	1,3333	-1,167	1,3333	0,3333	0,8333	0,3333	0,8333
	1,8571	-1,444	1,625	0,5238	0,2778	0,2917	0,5238
	2,0575	-1,765	1,8254	0,2004	0,3204	0,2004	0,3204
	2,2693	-1,932	1,9556	0,2117	0,167	0,1302	0,2117
	2,3833	-2,068	2,0503	0,114	0,1357	0,0947	0,1357
	2,4744	-2,153	2,1127	0,0911	0,0854	0,0624	0,0911
	2,5321	-2,214	2,1568	0,0577	0,0616	0,0441	0,0616
	2,5735	-2,256	2,1866	0,0415	0,0413	0,0298	0,0415
	2,6014	-2,284	2,2073	0,0278	0,0287	0,0207	0,0287
	2,6208	-2,304	2,2215	0,0194	0,0196	0,0141	0,0196
	2,634	-2,318	2,2312	0,0132	0,0135	0,0098	0,0135
	2,6431	-2,327	2,2379	0,0091	0,0093	0,0067	0,0093
Рис. 2.4. Решение системы линейных алгебраических уравнений методом Якоби с помощью программы Excel.

Дата добавления: 2015-07-25