Метод прогонки.

Применяется для решения систем уравнений с трехдиагональной (ленточной) матрицей. Такая система уравнений записывается в виде:

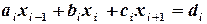
, (2.6)

.

Является частным случаем метода Гаусса и состоит из прямого и обратного хода. Прямой ход состоит в исключении элементов матрицы системы (2.6), лежащих ниже главной диагонали. В каждом уравнении останется не более двух неизвестных и формулу обратного хода можно записать в следующем виде:

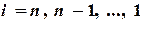, (2.7)

Уменьшим в формуле (2.7) индекс на единицу: и подставим в (2.6):

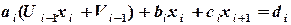
Выразим :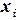

(2.8)

Сравнивая (2.7) и (2.8), получим:

(2.9)

Поскольку , то

, (2.10)

Теперь по формулам (2.9) и (2.10) можно вычислить прогоночные коэффициенты 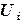и (). Это прямой ход прогонки. Зная прогоночные коэффициенты, по формулам (2.7), можно вычислить все 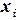() (обратный ход прогонки). Поскольку , то и . Далее вычисляем , ,..., , .

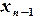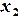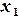Пример 2.3. Решить систему уравнений методом прогонки:

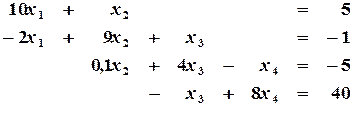
Решение. Коэффициенты записываем в виде таблицы 2.1.

				Таблица 2.1
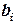
	-2			-1
	0,1		-1	-5
	-1

Прямой ход прогонки. По формулам (2.9) и (2.10) определяем прогоночные коэффициенты 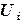и ().

, т.к.

Обратный ход прогонки. По формулам (2.7) вычисляем все 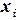(). Поскольку , то .

Далее вычисляем:

Вычисляем невязки ()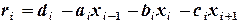

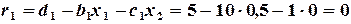
Алгоритм метода прогонки:

1. Ввести число уравнений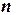

2. Ввести ().

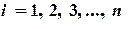3. Вычислить 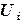и ; ().

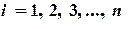4. Вычислить ().

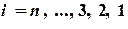5. Вычислить невязки ().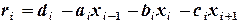

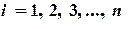6. Напечатать , ().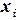

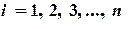На рис. 2.2 приведена программа решения методом прогонки.

CLC

Дата добавления: 2015-07-25