Изучение геометрических фигур

Запас знаний о геометрических фигурах постепенно обога­щается. По мере усложнения и увеличения разнообразия ви­дов деятельности ребенка расширяется кругозор, углубляется понимание связей, существующих между явлениями, проис­ходит постепенный переход к словесно-логическому мышле­нию.

Повторить и закрепить представления об уже изученных геометрических фигурах (круге, квадрате, прямоугольнике, треугольнике) можно в процессе различных упражнений, свя занных с делением фигур на части. Этот учебный материал соотносится с изучением долей.

Нужно показать, что если разрезать квадрат или прямо­угольник пополам по диагонали, то получатся два треугольни­ка. Если соединить длинные стороны треугольников (подби­раются прямоугольные треугольники), получится квадрат или прямоугольник. Если соединить короткие стороны треуголь­ников, то получится большой треугольник (рис. 21). Можно получить квадрат или прямоугольник из четырех треугольни­ков. Кроме этого, рассматривается деление квадрата пополам на два прямоугольника и получение прямоугольника из квад­ратов. Составить квадрат из двух прямоугольников можно только с определенным условием: короткая сторона прямо­угольника равна половине его длинной стороны.

Рис. 21

А.М. Леушина предлагает дать детям наборы фигур (круг, квадрат и треугольник), разделенных на две и четыре части по горизонтали, вертикали и диагонали (рис. 22).

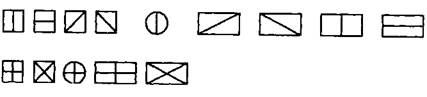
Каждая фигура с внутренней стороны должна быть окра­шена в особый цвет, а с другой, лицевой, стороны все фигуры и их части должны иметь одинаковый цвет. Виды упражнений с данным набором постепенно усложняются. Вначале дети составляют фигуры, разделенные пополам, с опорой на цвет.

Далее перемешивают части и дополняют их элементами тех же фигур, разделенных на четыре части, снова сортируют и составляют целое. Затем все фигуры и их части переворачи­ваются другими сторонами, имеющими одинаковые цвета, и из смешанного множества разных частей выбирают те, что нуж­ны для составления круга, квадрата и прямоугольника.

Предлагаются задания на соотнесение по форме предмет­ных картинок с геометрическими фигурами. Например, к кругу необходимо подобрать картинки с солнцем, мячом, колесом и др.

В процессе выполнения практических заданий проводит­ся повторение и проговаривание основных свойств и харак­терных отличий данных геометрических фигур.

Формирование представлений о четырехугольнике

Представление о четырехугольнике будет поверхностным, если при его изучении ограничиться обобщением знаний о квадрате и прямоугольнике. Поэтому, прежде чем приступить к рассмотрению четырехугольников, целесообразно познако­миться с ромбом и трапецией.

Формирование представления о ромбе начинается с рас­смотрения данной фигуры, обследованияконтура, выделения и подсчета количества углов, вершин и сторон. Однако этого недостаточно, чтобы понять его своеобразие. Необходимо из­мерить и сравнить длину сторон ромба. Полоску-мерку, подо­бранную так, чтобы она была равной по длине одной из сторон, последовательно прикладывают к сторонам ромба. Опреде­лив равные выбранной мерке стороны, необходимо взять дру­гую мерку-полоску и установить равенство двух других сто­рон. Дети узнают, что у ромба одинаковые две смежные сторо­ны (те, что имеют общую вершину).

Формирование представления о ромбе позволяет развить зрительное восприятие дошкольников. Важно научиться от­личать ромб от квад рата, находящегося в непривычном про­странственном положении. Поэтому воспитатель должен по­казать основные отличия квадрата и ромба, объяснить, что у квадрата все стороны имеют одинаковую длину, а у ромба толь­ко две. Кроме этого, выделить их сходство — квадрат и ромб имеют по четыре угла, вершины и стороны.

Ознакомление с трапецией проходит в процессе практиче­ской де ятельности, направленной на изучение своеобразия дан­ной фигуры. Дети должны провести пальцем по контору фигуры, пересчитать углы, вершины и стороны, проговорить название — трапеция. С ее особенностями можно познакомиться путем сопо­ставления с прямоугольником и треугольником (рис. 23).

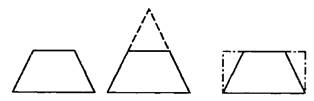
Для этого каждому ребенку предлагается взять треуголь­ник, вырезанный из бумаги (заранее подбирается равносторон­ний или равнобедренный), и отрезать верхний угол. Треуголь­ник со срезанным углом превратится в трапецию. При этом количество углов, вершин и сторон увеличится на одну. Далее берется бумажный прямоугольник и срезается левый и пра­вый верхний (или нижний) углы. Наклонный разрез прохо­дит от противоположной вершины. Получается, что у трапе­ции, как и у прямоугольника, четыре угла, четыре вершины и четыре стороны. Две противоположные стороны равны, но две другие имеют разную длину.

Трапеция имеет наклонные боковые стороны, а верхняя и нижняя стороны разные по длине. С помощью мерок-полосок дети должны самостоятельно установить их неравенство. Вос­питатель оказывает помощь в правильном речевом оформле­нии результатов практических действий и следит, чтобы вос­питанники проговаривали окончания превосходной степени сравнения и имен прилагательных, обозначающих длину сто­рон: «У трапеции нижняя сторона длиннее, чем верхняя сторона». Нужно показать, что трапеции могут быть разного размера и располагаться по-разному, например длинной сторо­ной вверху, а короткой вниз. Тогда можно сказать: «У трапе­ции нижняя сторона короче, чем верхняя».

Рассматриваются трапециевидные формы в окружающей действительности. Например, выкройка юбки, крышка жур­нального столика, крыша деревенского дома, наконечник печ­ной трубы, натянутая волейбольная сетка, чердачное окно, дно тележки для продуктов в магазине и др.

Наиболее важной является организация работы по обобще­нию знаний о геометрических фигурах. Необходимо показать сходства между квадратом, прямоугольником, ромбом и трапе­цией, обозначив их одним словом — четырехугольники.

Каждому ребенку предлагается взять квадрат, прямоуголь­ник, ромб и трапецию, пересчитать у них количество углов и назвать полученные результаты. Далее воспитатель поясняет, что у квадрата четыре угла, у прямоугольника четыре угла, у ромба четыре угла и у. трапеции четыре угла. У всех этих фигур по четыре угла, поэтому их можно назвать четырехугольника­ми. Повторение определяющей характеристики позволяет ус­воить новый математический термин, понять абстрактность его значения, активизировать интеллектуальную деятельность.

Данное обобщение усваивается детьми на сенсорно-пер­цептивном уровне, поэтому при его изучении высока роль на­глядного материала, практических действий и проговаривания способа их выполнения.

Для закрепления полученных знаний можно предложить следующие задания и дидактические игры:

• Из множества геометрических фигур выбери четырех­угольники.

• Назови, какие четырехугольники изображены на рис. 24.

Рис. 24

Положи слева от себя четырехугольники, а справа тре­угольники.

Объясни, чем отличается треугольник от четырехугольника. Объясни, почему прямоугольник можно назвать четырех­угольником.

Какие геометрические фигуры можно назвать четырех­угольниками. Почему?

Педагог раздает модели различных четырехугольников каждому ребенку. Называет четырехугольник: «У кого квадрат (трапеция, ромб и т.д.)?», а дети должны под­нять соответствующую модель. Если дети испытывают трудности в усвоении математических терминов, то педа­гог может не только называть четырехугольник, но и сам показывать соответствующую модель. Как можно назвать геометрические фигуры, изображен­ные на рис. 25?

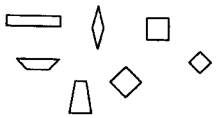
Рис. 25

• Назови квадрат, прямоугольник, ромб и трапецию одним словом.

• Что лишнее на рис. 26. Почему?

Рис. 26

• Составь узор, используя только четырехугольники.

• Игра «Геометрическое лото». Предлагается найти фигуру, аналогичную данной, независимо от ее величины и цвета.

• Игра «Найди свою пару». Необходимо заготовить два оди­наковых комплекта геометрических фигур одного цвета по числу детей. Педагог распределяет детей на две под­группы и размещает их в противоположных сторонах ком­наты. Детям каждой подгруппы раздают по одной форме из комплекта. По сигналу педагога они идут друг к другу, и каждый ищет свою пару, т. е. берет за руку того, у кого такая же геометрическая фигура.

• Рассмотреть, например, большой красный ромб и показать фигуру другого цвета и величины.

• Рассмотреть, например, маленький синий квадрат и пока­зать фигуру другой формы, но того же цвета и величины.

Положительные эмоции, возникающие во время игры, ак­тивизируют деятельность детей, обеспечивают решение задач, которые связаны с развитием произвольного внимания, памя­ти, познавательной функции речи, ассоциативной деятельнос­ти и формированием способности сравнивать, сопоставлять, делать выводы и обобщения.

Формирование представлений об овале

В старшей группе дается представление о фигурах оваль­ной формы. Это необходимо для систематизации фигур по род­ственным признакам и выделения фигур округлой формы.

Проводится ознакомление с контуром овала, анализ его структуры. В процессе практических действий по обследова­нию данной фигуры необходимо сделать заключение о том, что овал, как и круг, не имеет углов, но, в отличие от круга, у него одна часть широкая, а другая узкая.

А. М. Леушина предлагает раздать детям образцы (моде­ли) овала и круга разного цвета (высота овала должна быть равна диаметру окружности) и наложить их друг на друга. Такая работа наглядно показывает отличия и характерные признаки данных фигур (рис. 27).

Рис. 27

Рассматриваются овалы разной величины, предлагается раз­ложить их в убывающем и возрастающем порядке. Дается за­дание выбрать из множества геометрических фигур округлые фигуры, из округлых фигур — круги и овалы. Среди окружаю­щих предметов находятся те, что имеют форму овала, например скатерть, подушка, блюдо, поля шляпы и др. Анализируется фор­ма предметов на картинках (огурец, слива, яйцо и др.). Особое внимание уделяется построению речевых высказываний и вве­дению в речь слов «овал», «овальная форма» и однокоренных имен прилагательных: «овальный (стол)», «овальная (комна­та)», «овальное (блюдо)», «овальные (тарелки)». Проводится сравнение предметов по форме, например овального и круглого подносов, в ходе которого даются их словесные характеристики: «Этот поднос овальный, а этот — круглый».

Дата добавления: 2015-07-11