Изучение геометрических фигур. После рассмотрения геометрических тел следует присту­пить к формированию

После рассмотрения геометрических тел следует присту­пить к формированию представления о круге, квадрате, тре­угольнике. Изучению каждой из данных геометрических фигур нужно посвятить отдельное занятие, после чего провести их сопоставление, сравнение и дифференциацию.

Можно предложить следующий план изучения геометри­ческих фигур:

• Обследование фигуры по контору и ее название.

• Выделение и подсчет углов, вершин и сторон.

• Нахождение определенной фигуры разного цветы и раз­мера среди множества геометрических фигур, находящих­ся в различных пространственных положениях.

• Поиск предметов изучаемой формы.

• Сопоставление с другими фигурами и телами.

• Закрепление изученных форм на занятиях по рисова­нию, лепке, аппликации; составление геометрической ап­пликации.

Формирование представлений о круге

Круг рассматривается как проекция шара на плоскость. Детям можно в игровой форме (как рекомендует Л.Г. Петерсон) предложить посмотреть на шар в зеркало или «сфотогра­фировать» его. Если нарисовать полученное изображение, то перед детьми окажется круг. Сообщается название этой фор­мы и рассказывается о ее своеобразии, происходит обследова­ние ее модели (из дерева или картона) осязательно-двигатель­ным и зрительным путем.

Существенным признаком круга является отсутствие углов. После выделения данного существенного признака мож­но показать несущественные, такие как цвет и величину. Очень важно добиться понимания того, что данная фигура является кругом, независимо от цвета и величины. Для этого предлага­ется рассмотреть и сравнить большие и маленькие круги, раз­личные по цвету.

Обязательной является работа по нахождению данной формы в окружающей действительности. Воспитатель назы­вает форму различных предметов, просит показать круглые предметы, помогает детям составить и проговорить словосоче­тания. Например «круглое солнце», «круглый пирог», «круг­лая тарелка», «круглые обручи» и т. д.

Формирование представлений о квадрате

Квадрат является проекцией куба на плоскости, поэтому после актуализации знаний о кубе, обследования осязательно-двигательным и зрительным путем нужно обратить внимание детей, что в основании куба лежит квадрат. Далее проходит изучение модели квадрата (из дерева или картона). Дошколь­ники узнают название и своеобразие этой формы. При первом знакомстве с квадратом следует показать стороны, углы и вер­шины (рис. 18). Однако навык дифференцирования углов и вершин дети получат только в старшем дошкольном возрасте.

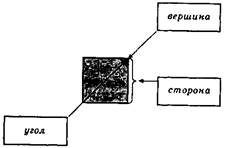
Рис. 18

Необходимо рассмотреть квадраты разного цвета и размера, найти эти фигуры в окружающей обстановке. Работа проходит по аналогии с заданиями, выполняемыми при изучении круга.

Ознакомление с квадратом осложняется тем, что дети не могут подсчитать точное количество углов, вершин и сторон. Их количество они смогут выяснить в средней группе. На данном этапе можно ограничиться сообщением, что углов, вершин и сторон в квадрате много, а после изучения треугольни­ка опосредованно определить, что у квадрата углов (вершин и сторон) больше, чем у треугольника, на один.

Формирование представлений о треугольнике

Для того чтобы дети получили обобщенное представление о треугольнике, необходимо организовать рассмотрение тре­угольников, отличающихся не только по цвету и величине, но и имеющих различную конфигурацию. Каждый ребенок дол­жен визуально и осязательно ознакомиться с разнообразными треугольниками, понять, почему все эти фигуры можно назвать одним словом: треугольники.

Детям названия разных видов не сообщаются, но они долж­ны уметь выделять из множества геометрических фигур лю­бой треугольник. Поэтому нельзя ограничить ознакомление с данной фигурой рассмотрением только одного вида. Воспита­тель заготавливает шесть треугольников (прямоугольный рав­нобедренный и разносторонний, остроугольный равнобед­ренный и равносторонний, тупоугольный равнобедренный и разносторонний) разного цвета и величины для демонстрации и работы каждому ребенку (рис. 19).

Дети рассматривают, изучают контуры всех фигур и под руководством взрослого определяют, что у них равное коли­чество углов, вершин и сторон, а также что углов и вершин столько, сколько сторон. Посчитать их количество они смогут только в средней группе, после изучения числа три.

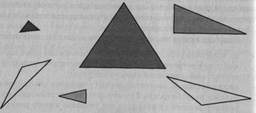
Рис. 19

Опосредованно можно сравнить численность углов, вер­шин и сторон треугольника. Около каждого угла предлагается положить, например, картинки с мячиком, а около каждой сто­роны — картинки с мишкой. Определить, что мишек и мячи­ков поровну. Значит, углов у треугольника столько, сколько и сторон.

Подобным образом сопоставляется количество углов у треугольника и квадрата. Около каждого угла треугольника следует положить картинку с яблоком, а около каждого угла квадрата — картинку с тарелкой. Приемом установления вза­имно-однозначного соответствия определить, что яблок мень­ше, чем тарелок, значит, углов у треугольника меньше, чем у квадрата. Аналогично сравнить по количеству вершин и сторон. Дети подводятся к выводу, что у квадрата углов, вершин сторон больше, чем у треугольника, на один.

По мнению Л.А. Венгера, Н.И. Непомнящей и др., использование опосредованного сравнения является важным условием для развития математических способностей в дошкольном детстве.

Закрепление знаний о треугольнике происходит в процессе дидактических игр и продуктивной деятельности.

Например, предлагается положить треугольник около пред­метов треугольной формы, которые есть в комнате (крыши игрушечных домиков, подставка для салфеток, головные убо­ры — косынки, колпаки, треуголки и др.).

Для развития словесно-логического мышления выполня­ются упражнения на классификацию фигур по форм е. Если ребенок не может выполнить задание само­стоятельно, то воспитатель помогает ему и поясняет действия: «Круги кладем к кругам, квадраты к квадратам, треуголь­ники к треугольникам. Здесь будут круги, здесь — квадра­ты, здесь — треугольники».

Дети младшего дошкольного возраста не могут длитель­ное время удерживать внимание на одном виде деятельности, поэтому количество фигур для классификации увеличивает­ся постепенно. Сначала используется набор из шести фигур (например, большой зеленый квадрат, круг, треугольник и ма­ленький красный квадрат, круг, треугольник). Постепенно чис­ленность фигур увеличивается. В старшем дошкольном воз­расте возможна классификация двадцати четырех фигур.

Классифицировать геометрические фигуры можно в про­цессе работы по подгруппам, что позволяет развивать комму­никативную деятельность. Под руководством педагога до­школьники учатся работать сообща, доказывать свое решение. Например, если ребенок положит круг к квадратам, то нужно не только его исправить, но и спросить, все ли согласны с та­ким решением, почему оно неправильно, и еще раз обратить внимание на то, что у квадратов есть углы, а у круга их нет. Это приучает анализировать действия, развивает навык самоконт­роля.

Уточнить и закрепить представления о формах можно так­же в процессе выполнения орнаментальных и сюжетных ком­позиций из разных геометрических фигур. Прежде чем при­ступить к работе, необходимо дать целостное представление о собираемом рисунке, рассмотреть его, проанализировать, из каких элементов он состоит, определить их место. При выпол­нении задания нужно попросить детей показать треугольник (круг, квадрат), дать название этой фигуре (если ребенок не может произнести ее название, воспитателю следует прогово­рить его громко, четко, по слогам, так, чтобы была видна арти­куляция).

Средняя группа

Дата добавления: 2015-07-11