
|
Читайте также: |
|
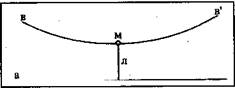
Вторично неявная напряженность геометрической поверхности проявила себя в геометриях Лобачевского и Римана. Это станет особенно заметно, если луч Л, входящий в точку М из прямой а, начинает двигаться вместе с точкой М на бесконечность, например в правую сторону (рис. 14). Причем граничные условия аксиомы запрещают точке приближение к прямой а, а лучу — сокращаться по длине, но не запрещают точке М удаляться, а лучу Рис. 14.
Л удлиняться (своего рода пространственное отталкивание). Поэтому по мере движения точка начинает отклоняться от прямой — ветвь в'. Если же луч Л вместе с точкой будет двигаться в левую сторону, то получим аналогичное откло-нение от прямой а — ветвь в. Фигура, образуемая обеими ветвями как бы единой прямой в, окажется не эквидис-тантой, а некоторой седловиной образуемой двусторонним движением.
В этом построении начинает проявляться физический смысл движения, и получается, что точка М замыкает на себя две самостоятельные ветви прямой в, разрывая ее и имея статус несобственной точки (точки одного ранга с прямой). Отсюда также следует, что пространство, в котором двигаются прямые, анизотропно. А потому луч Л, двигаясь от точки в любую из сторон, будет изменять свою длину пропорционально изменению напряженности пространства и движущейся точки. И также пропорционально этой напряженности будет меняться метричность отрезков по длине прямой вМв'.
Если же граничные условия (формулировка Римана) препятствуют отклонению ветвей в и в ' от прямой а при движении в обе стороны от точки М, то ветви, перемещаясь на бесконечность, будут приближаться к прямой а (рис. 15). Таким образом, граничные условия не позволяют образующему лучу в движении удлиняться, оставляя ему возможность сокращения. И в этих условиях луч Л выписывает подобие эллиптической кривой (своего рода пространственное притяжение). Однако конечные точки ветвей в, в' имеющие ранг прямой а, никогда не пересекут ее. И кривая вМв' никогда не будет иметь общей точки с прямой а. Она не замкнута.

|
Подобие линии вМв' эллиптической кривой послу-жило основанием для наречения римановой геомет-рии «сферической» и завуали-ровало как существование
Рис. 15. напряженности пространства, так и разрыв кривой в точке М. Поэтому образованная данной кривой, при вращении ее вокруг а, сферическая поверхность не может считаться истинной сферой и потому, что след точки М несет в себе момент нестыковки ветвей в и в', и потому, что эта "сфера" оказываетсянезамкнутой с линией а, и потому, что внутри "сферы" остается элемент образующей ее структуры — прямая а.
Напряженность, выражаемая элементами геометрии в виде неравноправных, несобственных точек и линий, по-видимому, снимается введением в геометрию понятия абсолюта — такой геометрической фигуры, которая остается неизменной при любых преобразованиях данной подгруппы. Следовательно, абсолютом считается элемент, ранг собственной напряженности которого выше остальных элементов данной плоскости. И все преобразования, изменяющие форму остальных элементов (и их напряженность), не в состоянии изменить напряженность абсолюта.
Таким образом, понятие абсолюта окончательно закрыло в геометрии все направления возможного описания реального мира в терминах напряженности, движения, взаимодействия. Геометрия стала чисто статическим описанием только одной актуальной бесконечности.
Попробуем в самой эскизной форме резюмировать некоторые первичные понятия и свойства элементов динамического пространства. Прежде всего, отметим важнейшую роль познания потенциальной бесконечности. Бесконечность как понятие высшая форма абстрагирования. Представление об осуществимости абстрактного движения в бесконечность приводит к противоречию с проявлением неопределенности и недостижимости в отдалении от нашего сознания. Движение в бесконечность оказывается абстракцией, связанной с возможностями качественного изменения дискретного пространства с переходом от пространства одного ранга к пространству другого ранга. Именно ранжирование бесконечностей по уровням определяет соизмеримость или несоизмеримость пространственных образований или отрезков прямых.
Иерархическая равнозначность ранговых структур по их положению и естественное взаимодействие при движении определяет дискретность и непрерывность образуемого ячейками пространства плоскости или объема. Ячеистое поле пространства само для себя и для своего ранга дискретно, а для верхнего ранга непрерывно и носит полевой характер. Динамическое пространство всегда не пусто.
Естественный смысл бесконечности заключается в ее количественной и качественной незавершенности. Это выражается, в частности, через изменение метричности в сопоставлении с метричностью статической геометрии. Каждый последующий шаг всегда отличен от предыдущего качественно и количественно.
Как только вводится понятие бесконечного пространства, т.е пространства имеющего другое качество, и элементы геометрических фигур устремляются в бесконечность (например, пятая аксиома в формулировке Евклида), тем самым в статическую геометрию неявно вводятся новые, не присущие ей качества (движение, недостижимость бесконечности, неопределенность, время, взаимодействие и т.д.). И эти качества коренным образом изменяют поведение геометрических элементов и пространства, которое описывается ими. Эти качества приводят к взаимосвязи всех элементов движения и геометрическая статическая общность точек, отрезков, плоскостей, объемов сразу наполняется физическим содержанием и становится разделом физики; системной общностью. Общностью, в которой ни одна точка, ни одна фигура ни в одном месте пространства не обладает истинной самостоятельностью, оставаясь в то же время равновеликой по значимости и взаимодействию со всеми фигурами и пространством. И всякое ее движение в любом направление этого пространства будет сопровождаться изменением ее геометрических (статических) параметров пропорционально напряженности самого пространства. Однако динамические (физические) параметры этой общности останутся неизменными. И эти качественные противоречия изменяемости и неизменности параметров в статическом и динамическом состояниях тоже неявно заложены в пятую аксиому Евклида.
Имеются неоднозначности и в соизмеримости расстояния в пространстве между двумя произвольными точками А и В. Хотя оно и в одном и в противоположном направлении количественно равно (понятие расстояния применено здесь по аналогии с Евклидом), но не эквивалентно и потому не отвечает требованиям рефлективности, симметрии и транзитивности (следствие неоднородности и анизотропности пространства), оно не может быть взято безотносительно времени и плотности, которые в неявном виде присутствует в каждой области пространства.
Перенос отрезков или фигур параллельно своему положению вдоль замкнутого контура вызывает их постоянное самотождественное изменение, но в результате обхода контура конечная фигура совпадет с первичной. В пространстве отсутствуют малые поверхности и объемы (относительно измерителя), и перенос фигуры или мерного инструмента из одного пространства в другое вызывает изменение длины мерных инструментов (относительно статики) пропорционально напряженности внешнего поля данного пространства. Сумма же углов треугольника и на поверхности сферы, и в объеме всегда равна 2 π. Эта особенность исключает возможность определения разницы в геометриях. Отличительная особенность динамического пространства и образованного им пространства — детерминизм. Именно каузальность порядка причина-следствие определяется коэффициентом связности и золотым многообразием.
Рассмотрим основные фигуры пространства. Все материальные образования одного ранга, кроме продуктов катастроф, стремятся приобрести форму сферы. Сферы одного пространства обладают следующими качествами:
• все, сферы построенные вокруг отсутствующего единого центра, равны. Их эквипотенциальная поверхность состоит из бесчисленного количества ячеек, а радиус имеет бесконечную длину;
• каждый отрезок исходит из точки и входит в другую точку. Однако их можно продолжить по прямолинейной поверхности сферы до исходящего отрезка и считать непрерывными;
• сферы всегда ядра и на плоскости и в пространстве различаются по рангу. Сферы более «низкого» ранга могут считаться точками. Точка — это всегда материальная сфера, не имеющая центра.
Точка — ядро, структура которого несоизмерима по рангу с пространством, в котором она находится, и влияющая на это пространство. Внешняя поверхность отграничивает ее от пространства. Точка всегда бесконечна вглубь. Точка на прямой или в пространстве и луч из нее — это отделение соизмеримой области пространства (внешняя часть образующегося луча) от несоизмеримой (части, устремленной к центру точки).
Все точки одного ранга неравнозначны по количественным величинам всех качеств и в первую очередь по напряженности. Поэтому метрика координатных осей с центром в любой окрестности точки, кроме ядра, будет различной (относительно статического эталонного метра).
Ячейка (две или более) — взаимосвязанные напряженностью собственного поля сферические структуры (ядра), несоизмеримые по размерам с расстояниями между ними, входящие в единую внешнюю эквипотенциальную нейтральную зону. Все пространство — «пена» взаимосвязанных первичных ячеек.
Линия (прямая) — абстракция — последовательность расположенных в одном направлении несоизмеримых с пространством ячеек. Линия всегда дискретна. Дискретность обусловлена наличием бесконечных (вглубь) точек на ней. Непрерывной она может быть только мысленно.
Поверхность (плоскость) — многообразие распространяющихся в двух направлениях дискретных ячеек.
Объем — область, образованная состоянием взаимосвязанных ячеек, отграниченная от других областей своей нейтральной зоной. Существование нейтральных зон определенной напряженности обусловливает свойства каждого из тел
2.4. Геометрия золотых пропорций
Откуда пришли представления о делении отрезков в крайнем и среднем отношении, позволяющем получать золотое число Ф и образующие пропорцию, названную Леонардо да Винчи «золотым сечением», неизвестно. Ho в Древней Греции на основе золотого числа Ф = 1,618 получали ряд из 11 чисел посредством последовательного умножения базисной 1 на Ф (восходящая ветвь ряда) и делением базисной 1 на Ф (нисходящая ветвь ряда), имеющий название золотого ряда и бесконечный, при продолжении, в обе стороны:...; 0,034; 0,056; 0,090; 0,146; 0,236; 0,382; 0,618; 1,000; 1,618; 2,618; 4,236;... и т.д. (египетский ряд [28 ]). Каждое число этого ряда представляет собой иррациональную (бесконечную) последовательность цифр, округленных до 4 знаков. Каково собственное значение этих чисел, и к какой геометрии они относятся — неизвестно тоже, а потому числа эти стоят на обочине и геометрии и физики.
Золотое число Ф = 1,618... получается несколькими способами, оно из которых — деление отрезка в крайнем и среднем отношении. Отметим, что в постановке задачи говорится о делении одного отрезка на две неравные части а и с так (рис. 16), чтобы весь отрезок (а + с) относился к большей части с, как с к меньшей части а. Запишем это отношение:
(а + с)/с = с/а (2.1)

|
| Рис. 16 |
Пропорция (2.1) носит название золотой. В данном случае подразумевается конечная в рациональных числах длина отрезка (а + с), кратная некоторому измерительному инструменту. В условии задачи нигде не говорится о невозможности его целочисленного или дробного рационального деления и о нерациональности двух (?) образующихся при делении отрезков.
Это очень важная оговорка. Она подтверждает непреднамеренный, а как бы вероятностный или даже случайный характер деления. Проверим эту случайность. Проведем решение (2.1), заменив отношение с∕а нa b:
b = c / a, (2.2)
и, подставив (2.2) в (2.1), получаем квадратное уравнение
b2 – b – 1 = 0, (2.3)
решая которое, находим величину b:
b1 = (1 + √5) / 2= Ф = 1,6180339, (2.4)
b2 = (l – √5)/2 = – 1/ Ф = – 0,6180339. (2.4)
Золотое число Ф – является числом иррациональным. То есть таким числом, бесконечная последовательность которого не может быть вычислена до конца, сколько бы времени его ни вычисляли.
Отмечу, что любое иррациональное число — не количественное число. Оно индивидуально, не имеет однозначного количественного выражения и отображает своего рода математическое качество. Оно отражает неограниченную количественную величину и не может точно складываться как с рациональными, так и с иррациональными числами (качества не складываются). Оно квантованный (выделенный из числового ряда) элемент числового ряда, обособленный от него и не примыкающий ни к одному большему или меньшему числу. Все операции с ним проводятся с приблизительной точностью. Повторяю — это качественная индивидуальность, и, следовательно, бесконечный ряд иррациональных чисел не является дурной бесконечностью. С нахождением иррационального числа в математику входит представление о математическом качестве и квантовании чисел, вне зависимости от того, осознали это математики или нет. Квантованное иррациональное число — основа и предтеча квантованной геометрии. Но вернемся к Ф.
Получив Ф и ее обратную величину, т.е. два числа, мы успокаиваемся, так и не определив, а чему же равны числа а и с в формуле (2.1) и какое отношение они имеют к b, тем более, что подстановка b в (2.2) с последующим выходом на (2.1) не приводит к определению величин а и с, а следовательно, и не решает поставленную задачу.
Тогда зачем же мы находим b?Ответ — только для того, чтобы получить точную величину Ф, поскольку знаем, что это число — основа золотой пропорции. Но что скрывает это число? В чем суть золотой пропорции?
Попробуем решить (2.1) другим путем. Умножим числитель и знаменатель левой части отношения (2.1) на а, правой на с и, сократив знаменатели, получаем следующее уравнение:
а2 + ас = с2. (2.5)
Уравнение (2.5) по количественной величине а и с оказывается полностью неопределенным. Ее члены, хотя и зависимы друг от друга, могут составлять пропорции при любых числовых значениях одного из них. Если же в (2.5) вместо ас подставить
b2 = ас, (2.6)
то уравнение (2.5) из простой пропорции превратится в теорему Пифагора:
а2 + b2 = с2. (2.7)
Поскольку операция замены ас на b2 при данных ограничениях возможна только в единственном случае, когда а = √Ф, то в исполнении (2.7) числа а, b, с оказываются однозначно связанными с золотым числом Ф. И, как следствие, члены уравнения (2.7) становятся геометрически квантованными относительно золотого числа. Какую бы количественную величину они не имели они всегда остаются степенью числа Ф. Появление квантованной по золотому числу Ф геометрической зависимости свидетельствует о возможности построения геометрии на квантованных числах или, иначе говоря, о возможности построения квантованной геометрии. Но вернемся к уравнению (2.7), которое описывает равенство суммы квадратов катетов прямоугольного треугольника квадрату гипотенузы. В нем индекс b численно отображает большой катет прямоугольного треугольника. И, следовательно, деление в крайнем и среднем отношении есть деление не на два отрезка, а на три, в пропорциях прямоугольного треугольника, в котором число b = Ф неявно занимает место одного из катетов. И вместо двух отрезков мы как бы получаем три, образующих новое геометрическое качество — прямоугольный треугольник. Наличие отношений (2.2) и (2.6) свидетельствует о существовании еще одного числа i, кратного а, b, с. Для получения i возведем в квадрат (2.2) и, подставляя в него значение b2 из (2.6), имеем:
а2 ·ас = с2, (2.8)
с = а3.
Подставляя величину с из (2.8) в (2.2), получаем:
b = а2.
И окончательно:
a6 = b3 = c2.
Поскольку b имеет два значения b1 = 1,618, и b2 = 0,618, то по ним находим i1, i2:
i1 = b31 = (1,618)3 = 4,2358,
i2 = b32 = (0,618)3 = 0,236.
Извлекая из i1 и i2 корень шестой степени, получаем количественную величину а1,а2:
а1 = 6 √ i1 = 6√4,236 = 1,272,
а2 = 6√ i2 = 6√0,236 = 0,786.
Проведя извлечение квадратного корня из чисел i, находим значения с:
с1 = √i1 = 2,058,
с2 = √i2 = 0,4858.
Выясним, какой модуль по длине, рациональный или иррациональный, имеет отрезок, делимый в крайнем и среднем отношении:
с1 + а1 = 3,33019... = а15.
Таким образом, в среднем и крайнем отношении делятся только иррациональные отрезки. А это может обозначать одно — все естественные отрезки сами по себе и сами для себя имеют свою иррациональную метрику, несоизмеримую со стандартной (декретной) метрикой.
Следует обратить особое внимание на то, что способ деления отрезков в крайнем и среднем отношении с использованием теоремы Пифагора, по-видимому, единственный, обусловливающий нахождение восьми взаимосвязанных и пропорциональных Ф золотых чисел, образующих новый ряд, отличающийся от египетского пропорциональностью каждого числа «коэффициенту» 1,272...:
... 0,183; 0,236; 0,300; 0,382; 0,486; 0,618; 0,786; 1,000; 1,272; 1,618; 2,058; 2,618; 3,330; 4,236; 5,388;...
Этот удивительный бесконечный ряд иррациональных чисел, названный русским рядом, образующий набор подобных прямоугольных треугольников при придании любой последовательности троек чисел (например, 2,058; 2,618; 3,330; или 0,185; 0,236; 0,300) значимости отрезков. Треугольники образуются и при последовательном сдвиге чисел на одну или две цифры (например, 2,058; 2,618; 3,330 - один треугольник; 2,618; 3,330; 4,236 - другой; 3,330; 4,236; 5,388 - третий и т.д.) Создается впечатление, что они как бы нанизываются друг на друга, образуя невидимую цепочку.
Существование в золотом ряду чисел-отрезков, способных образовывать прямоугольные треугольники, не может быть случайностью. Похоже, что они выполняют какую-то неизвестную нам функцию, определяемую степенями и последовательностью чисел ряда.
Но можно представить и другую картину. Имеется два ортогональных бесконечных катета, пересекаемых на пропорциональном иррациональном расстоянии параллельными линиями, отрезки которых превращаются в гипотенузы. А это уже не цепочка, а плоскость. И сразу же возникает предположение, что прямоугольные треугольники есть элементы прямоугольников, а их катеты — стороны прямоугольников. Продолжение катетов — оси координат х и у на плоскости, а гипотенузы — диагонали образовавшихся прямоугольников. И прорисовывающаяся естественным образом координатная сетка начинает походить на истоки некоей новой геометрии. Посмотрим, что еще скрывается в этом ряду.
Вернемся к теореме Пифагора об образующей плоскости и построим ее объемный аналог в трехмерном евклидовом пространстве. Проиндексируем любую последовательность из четырех чисел русского ряда исходя из того, что каждые три числа последовательности образуют прямоугольник с двумя сторонами и диагональю: х, у, l, п, где l и n диагонали прямоугольников х, у, l и е, l, п. Они образуют следующие пропорции:
x2 + y2 = l2,
yо2 + l2 = п2.
Здесь у по количественной величине равно уо, но ортоганально ему и х, а потому не складывается с у. Но будучи ортогональной плоскости ху, уо приобретает качество третьей координаты – z, и потому, приравняв z = уо, получаем плоскостной аналог теоремы Пифагора для «трехмерного» пространства:
х2 + y2 + z2 = п2. (2.9)
Перед нами достаточно странное уравнение (2.9). Числа одного математического ряда своей взаимосвязью демонстрируют изменяемую по длине пространственную (объемную?) структуру (струну?), у которой поперечное сечение тоже изменяемая, но равная по высоте и ширине, скрытая за индексацией величина.
В отличие от общепринятой системы координат, индексация которой может содержать произвольный набор чисел, уравнение (2.9) составляется только из четырех иррациональных взаимосвязанных последовательных чисел русского ряда и по своему характеру является квантованной системой, т.е. качественно новым математическим образованием. Возникает вопрос: Случайно ли получается квантованная координатная система? Или она может послужить основанием для построения квантованной геометрии? Для ответа на этот вопрос продолжим преобразования уравнения (2.9). Перенесем все ее индексы в правую часть и получим запись одинаковую по форме как для динамической, так и для статической геометрии:
0 = п2 – х2 – у2 – z2. (2.10)
Рассматривая уравнение статической геометрии (2.10) Гильберт и Клейн предположили, что если приравнять п2= 1, то может существовать геометрия, в которой (2.10) имеет следующий вид:
0 ≠ 12 – х2 – у2 – z2. (2.10′)
Поскольку правая часть уравнения не равна 0, то вместо 0 можно поставить s2, и уравнение принимает вид:
s2 = l2 – x2 – y2 – z2. (2.11)
Геометрия с таким основанием была названа псевдоевклидовой геометрией. Именно ее использовал Минковский для введения «четвертого» измерения — времени t посредством приравнивания l2 = с г:
s2 = с2t2 – х2 – у2 – z2. (2.12)
И это уравнение (2.12), отображающее не четырехмерный объем, а «рассечение» трехмерного пространства пятью плоскостями утвердилось в науке под названием «четырехмерный мир Минковского». Однако ни уравнение (2.11) ни (2.12) не являются аналогами уравнений динамической геометрии (2.9) и (2.10), поскольку в них за координатной индексацией могут скрываться любые комбинации не связанных между собой чисел как рациональных, так и иррациональных (Например, квадрат произведения времени на скорость никак не связан с квадратами координатных осей.) А уравнения (2.9) и (2.10) образуются только иррациональными числами любых трех последовательных чисел русского ряда. Ни s ни п в данное уравнение, по-видимому, ввести невозможно, поскольку другие члены ряда не образуют соответствующих пропорций. И чтобы осуществить подстановку п в (2.10) так, чтобы получилось равенство вида п2 = 12 – s2, необходимо «выйти» за пределы русского ряда во вне, отыскать матрицу, содержащую поле взаимосвязанных иррациональных чисел и включающую в свою структуру русский ряд. И такая матрица была найдена еще до рассмотрения данного ряда. Это русская матрица [28,30].
2.5. Структура русской матрицы
С русской матрицей мне пришлось познакомиться при изучении секретов старинных измерительных инструментов — древнерусских саженей. Необъяснимой особенностью этих инструментов являлось то, что их было много (десятки), они были несоизмеримы между собой, и при разметке объекта не допускалось разбиение осевых (координатных) размеров одной саженью. Разметка обязательно проводилась, начиная с высоты (координата – z) одной саженью, далее ширины (координата – х)— другой саженью и, наконец, длины (координата – у) — третьей саженью. Все оси разбивались только четным числом саженей. Было непонятно: зачем и как пользоваться десятками саженей, осложняя работу? Почему саженей много, разве нельзя обойтись одним измерительным инструментом? Почему они несоизмеримы между собой? Как могла сложиться такая архаичная система измерения? Почему она оставалась в употреблении в течение многих тысячелетий? И т. д. На эти многочисленные вопросы десятилетиями не находились ответы.
Однако А.А. Пилецкий [30] сумел свести все многообразие не пропорционированных друг другу древнерусских саженей к 15 типоразмерам, показать, что все они пропорциональны золотому числу Ф и подойти к построению матрицы, отражающей их взаимосвязи, используя для этого применяемый только на Руси метод раздвоения-удвоения для получения из саженей более мелких измерительных инструментов. (По методу сажень делилась надвое, получалось полсажени, полсажени надвое — локоть и так далее до вершка. На вершке деление заканчивалось.) Именно метод раздвоения удвоения привел к воссозданию русской матрицы (подробнее [30, 31]). Приведу фрагмент русской матрицы (матрица 1).
Матрица 1.
| 9,609 | 8,643 | 7,774, | 6.992 | 6,289 | 5,567 | 5,088 | 4,576 | 4,116 | 3,702 | 3,330 |
| 6,795 | 6,111 | 5,49" | 4,944 | 4,447 | 4,000 | 3,598 | 3,236 | 2,911 | 2,618 | 2,355 |
| 4,804 | 4,321 | 3,88" | 3,496 | 3,145 | 2,828 | 2,544 | 2,288 | 2,058 | 1,851 | 1,665 |
| 3,397 | 3,056 | 2,748 | 2,472 | 2,224 | 2,000 | 1,799 | 1,618 | 1,455 | 1,309 | 1,177 |
| 2,402 | 2,161 | 1,942 | 1,748 | 1,572 | 1,414 | 1,272 | 1,144 | 1,029 | 0,9256 | 0,8325 |
| 1,699 | 1,528 | 1,374 | 1,2361 | 1,112 | 1,000 | 0,8994 | 0,8090 | 0,7277 | 0,6545 | 0,5887 |
| 1,201 | 1,080 | 0,97170,8740 | 0,7861 | 0,7071 | 0,6360 | 0,5721 | 0,5145 | 0,4628 | 0,4163 | |
| 0,8493 | 0,7693 | 0,6871 0,6180 | 0,5359 | 0,500 | 0,4497 | 0,4045 | 0,3638 | 0,3272 | 0,2943 | |
| 0,6006 | 0,5402 | 0,4869 0,4370 | 0,3990 | 0,3536 | 0,3180 | 0,2860 | 0,2573 | 0,2314 | 0,2081 | |
| 0,4247 | 0,3820 | 0,34360,3090 | 0,2779 | 0,2500 | 0,2249 | 0,2022 | 0,1819 | 0,1636 | 0,1472 | |
| 0,3003 | 0,2701 | 0,24290,2185 | 0,1965 | 0,1768 | 0,1590 | 0,1430 | 0,1286 | 0,1157 | 0,1041 |
Основу структуры русской матрицы 1 составляет двойная крестовая последовательность записи чисел, при которой центр матрицы образует базисная 1 (единица), и в одной с ней строке находятся цифры горизонтального ряда, а перпендикулярно ей вертикальный (базисный) ряд, формирующий числовое поле матрицы, начинающийся с рационального или иррационального числа. По диагонали через 1 снизу вверх слева направо — диагональный ряд, начинающийся либо с золотого числа Ф, либо Ф в степени, либо степень от него. Числовое поле матрицы распространяется в бесконечность во все направления. Таким образом, матрицу формируют три числа:
Дата добавления: 2015-07-11; просмотров: 87 | Нарушение авторских прав