Пульсация единственное в природе движение тел относительно самих себя, пространства и других тел, их прирожденное свойство. Это третий и опре­деляющий вид движения. 4 страница

Предположим, что из точки А к точке О движется тело-точка и за прошедшее время она прошла расстояние АА, след- траектория которо­го есть прямая ли­ния. Будем назы­вать ее прямой. Одновременно из точки А' к тому же центру О движется другое тело-точка. И эта точка прошла расстояние А'А'. Ее след-траектория тоже прямая линия или просто прямая,

Рис. 8

как и след всех последующих точек. Прямые АА и А'А', ос­тавленные движущимися точками, по геометрии Евкли­да не являются параллельными.

Но в динамической гео­метрии они параллельны, поскольку никогда не в состоянии достичь центра О и, следовательно, пере­сечься в одной точке. К тому же, в отличие от «прямых» Лобачевского и Римана, они действительно прямые. Определим, какие зависимости возникают между дви­жением этих прямых и элементами фигур, образуемых ими. Продолжим построение (рис. 9). Проведем допол­нительные прямые АА', А"А",... АⁿАⁿ так, чтобы по длине они оставались равными между собой, а расстоя­ние между ними определялось отрезком, выходящим из некоторой точки k прямой АА до точки k', лежащей на прямой А'А' под углом Akk' к прямой А′А' и равным ему углом А'kk' прямой АА.

След следующей прямой проводим по тем же правилам из точки k ' прямой А'А' к точке k" прямой А"А". И так до тех пор, пока отрезок, выходящий из точки kⁿ прямой А^пАⁿ, не замкнет построение ломаной на прямой АА. Поскольку расстояние между прямыми одина­ково, а углы на пересе­чении каждого отрезка с прямой равны, замы­кающий отрезок попа­дет в ту же точку k прямой АА, из которой вышел отрезок kkⁿ. Замкнутая ломаная kk'k"...кⁿ образует равносто­ронний многоугольник. В результате получаем на плоскости «частокол» пря­мых, имеющих своим стремлением недостижимый в бесконечности, а потому фиктивный, центр О. Все пря­мые в своем движении к недостижимому центру парал­лельны и по определению и по структуре напряженно­сти на поверхности плоскости. А основная особенность образовавшегося правильного многоугольника ¾ дихо­томия конечного и бесконечного в том, что конечный периметр замыкает в себя площадь бесконечной вели­чины. Если теперь через центры отрезков, образующих стороны многоугольника kk′ k'k", k"k"',…, kⁿk, провести новые прямые и соединить их отрезками по правилам, изложенным выше, то получим многоугольник с коли­чеством сторон, превышающем количество первого в два раза. При продолжении этой операции бесчисленное число раз длина отрезков kk', k'k",..., k"k будет стремиться к минимуму, а углы Аkk', А'k'k′′ А′'k′'k′",... устремятся к π/ 2, и в пределе многоугольник kk′k′′ …kⁿ долженпревратится в окружность на плоскости. Плоскость окружности одно­временно будет обладать свойствами евклидовой стати­ческой геометрии, и содержать в своих границах пло­щадь конечной величины, и свойствами неевклидовой геометрии и содержать в тех же границах площадь ве­личины бесконечной. Две несовместимые площади как бы налагаются друг на друга.

Рис. 9.

В полном соответствии с геометрией Евклида длина окружности S будет равна 2 π радиан, а радиус, напро­тив, будет стремиться к бесконечности, никогда не дос­тигая центра О. Последний в данном случае, отсутству­ет. Прямая может исходить из какой-то точки окружности или входить в нее, но никогда не может пройти бесконечность. В то же время, по геометрии Евклида, центр у данной окружности S имеется, длина ра­диуса R конечна и определяется уравнением R = S/ 2 π.

Получается, что одни и те же геометрические элемен­ты можно одновременно мерить и жесткими стержнями (геометрия Евклида) и динамическими. А это означает, что между геометрией статической и динамической имеется определен­ная взаимосвязь. Попробуем ее отыскать.

Отложим от точки k вправо и влево (см. рис.9) по от­резку kk₁ и kk₂ одинаковой длины в евклидовой мерно­сти и, используя предыдущее правило построения, про­ведем через них еще две окружности k₁'k₁"k₁′"... k₁ⁿ и k₂′k₂′′k₂′′′… k₂ⁿ. Естественно, что окружности k₁ и k₂ по от­ношению к окружности k будут описанной и вписанной. И это единственное, что общее, как для евклидовой, так и для неевклидовой геометрии.

Отличие же их начинается уже с того, что наружу от окружности обе геометрии допускают проведение бес­счетного числа окружностей на одинаковом расстоянии друг от друга, а внутри окружности k, по геометрии Евклида, число таких окружностей ограничено, для динамичёской же геометрии — снова не ограничено. Каж­дая окружность — эквипотенциальная линия относительно точки О. И длина ее (или окружность) равна бес­конечности одного ранга, т.е. они равны между собой. Это есть следствие аксиомы о динамических параллель­ных. Оно может быть сформулировано следующим об­разом:

Дуги-хорды kk', k₁k₁′, пересекающие прямые АА и А'А' под одним углом и на некотором расстоянии друг от друга, имеют одинаковую длину.

Это следствие — теорема требующее доказательства. В настоящей работе она предлагается как аксиома. И на ее основе получается, что:

• В геометрии Евклида длина всех окружностей раз­лична, а в неевклидовой одинакова. Линия же окружно­сти является прямой.

• В геометрии Евклида линия окружности непрерыв­на, а в неевклидовой дискретна и состоит из бесчислен­ного множества одинаковых отрезков бесконечной дли­ны.

• В статической геометрии радиус окружности коне­чен, в динамической бесконечен.

• В статической геометрии взаимодействие между ра­диусом и окружностью отсутствует, в динамической на­личествует.

• Статическая геометрия радиусы и окружности не связывает со временем, в динамической такая связь имеется и т.д.

Таким образом, отсутствие одинаковых качеств у ок­ружностей двух геометрий лишает нас возможности оп­ределения взаимосвязи между ними по качественным признакам и вынуждает использовать свойства несоиз­меримых чисел (что вполне понятно, поскольку конеч­ное и бесконечное несоизмеримы по определению). Возьмем, например, два евклидовых круга одинакового радиуса r и площадью S. Сложим площади вместе так, чтобы образовался новый круг в два раза большей пло­щадью S' и определим, насколько радиус R нового круга больше радиуса r маленького круга. Площадь большого круга S'= πR², малого S = πr²:

πR² = 2 r²π R = r√2= 1,41421... r.

Число √2, по Дедекинду, и есть несоизмеримое ирра­циональное число, символ особого способа распределе­ния соизмеримых чисел [9]. В динамической геометрии, однако, это символ связности, а в данном случае — каче­ственный коэффициент, обусловливающий изменение пространства при движении в нем двух линий к отда­ленному центру. При коэффициенте связности, равном √2, две линии, движущиеся на плоскости к одному цен­тру, всегда параллельны, или, что то же самое, никогда не пересекаются на бесконечности. При устремлений √ 2→ 1 соизмеримость бесконечности меняется, и при достижении 1 динамическая геометрия переходит в статическую геометрию Евклида на плоскости.

Определим, чему равно несоизмеримое число, описы­вающее пространство. Используем метод построения окружности при образовании сферы. Для этого прове­дем множество одинаковых прямых АА, параллельных А′А′, направленных к единому центру, но не в плос­кости, а в объеме, и получим «ежик» прямых, устремленных в одну точку, на бесконечности. Пересечем их прямыми, исходящими из точки k₁, по ранее описанному методу. В результате по­строения получаем сферический многогранник, Сходя­щийся при бесчисленном увеличении граней в правиль­ную сферу, имеющую конечную площадь поверхности, но бесконечную длину радиуса.

Имеется и более простой способ построения сферы путем вращения образовавшегося круга вокруг прямой, например, АА (Рис. 9.), становящейся осью вращения, а при повороте на минимальные градусы «втыкаются» прямые, направленные к центру. Но при этом создается иллюзия, что образовавшаяся сфера име­ет выделенную ось вращения, и ось эта — прямая, про­ходящая через центр сферы. В данной же сфере ни одна прямая, входящая в сферу и идущая к центру, до него не доходит и тем более его не проходит.

Любым из этих способов можно построить бесчис­ленное количество сфер как внутренних, так и внешних по отношению к базисной сфере k, объем каждой из ко­торых будет конечен в евклидовой геометрии и беско­нечен в динамической. И если объем всех евклидовых сфер геометрически различен, то объем неевклидовых сфер физически равен друг другу, т.е. обладает тем же соотношением качеств, что и окружности.

Теперь, исходя из метричности евклидовых объемов сфер, определим величину коэффициента объемной связности (объемное число Дедекинда). Мысленно вы­членим внутри одной сферы V другую таким образом, чтобы объем вычлененной сферы V_о и объем сферы V₁ между поверхностями двух сфер были равны: V = V_о, тогда суммарный объем V равен:

V = 4/3 πR³ = V₁ + V = 2 V = 8 / 3 πR³.

Определим, насколько радиус внешней сферы R превы­шает радиус внутренней r, R³ = 2 r³.

Отсюда: R = ³√2 r = 1,259921... r. k = 1,259921.

Таким образом, коэффициент связности объема k (не­соизмеримое число Дедекинда) равно: k = ³√2 = 1 259921.... Это число, как и коэффициент связности окружности, является иррациональным и обусловливает бесконечное движение параллельных к центру сферы.

Хотя коэффициент связности и является безразмерностной величиной, он качественно индивидуален для каждого параметра. Говоря словами Дедекинда, каждый коэф­фициент принадлежит своему и только своему рангу па­раметров, а потому для каждого из них необходима соб­ственная индексация.

2.2. Структурирование динамического

пространства

Известно, что проблема бесконечного включает дихо­томию взаимосвязи двух пар категорий, с одной сторо­ны, различие конечного и бесконечного, с другой — по­коя и движения. Попарное существование противо­положных форм категорий обусловливает различие в подходе к описательному отобра-жению космических тел и структур. Это различие прежде всего относится к первичным понятиям: тело-точка, прямая-луч, плос­кость, движение и т.д.

Выше было показано, что тело в динамической гео­метрии представляет материальную сферу, бесконечную внутрь и отграниченную собственной поверхностью от окружающего пространства. Тело, как вещественное об­разование, формирует структуру и влияет на внешнее пространство в соответствии с энергетической на­пряженностью, создаваемой количественной величиной всех своих свойств.

Тело можно представить точкой только тогда, ко­гда ее параметры и собственная напряженность несо­поставимы по рангу с параметрами и напряженностью окружающего пространства и тел, образующих структуру данного пространства.

Линия или прямая есть условный след от движения точки (тела) в пространстве. И начало и конец линии входят в поверхность некоторых точек. Линии на уча­стке от поверхности одной точки-сферы до другой имеют конечную длину изменяемой метричности, отождествляемую с некоторой метрической цифрой.

Если эту же прямую продолжить за пределы поверх­ности конечных точек-сфер, внутрь их, то прямая станет иметь бесконечную длину, не отождествимую ни с какими действительными числами.

Линия (условная), соединяющая две движущиеся оп­ределенным образом точки, называется образующим лучом или образующим. Образующий луч индексируется начальной буквой слова — Л. Так, если одна из точек не­подвижна на плоскости, а другая, не меняя расстояния до первой, описывает в движении правильный круг, то образующий луч с такими свойствами в геометрии на­зывается радиусом.

В пространственных системах образующий луч Л всегда подвижен, и каждая его точка в процессе движе­ния описывает геометрическую фигуру, соответствую­щую уравнению движения и коэффициенту связности. Естественно, что в уравнении движения зашифрована и напряженность области концевых точек луча и про­странства, в котором луч движется. (Везде предполага­ется, что след движения остается только от перемеще­ния концевых точек.)

Основной способ движения луча в динамической геометрии — собственное удли­нение или сокращение (пульсация) с

определенным пе­рио-дом, сочетающийся с вращением и некоторым про­странственным переме-щением, например в простран­стве декартовых координат. Поэтому кривые Рис. 10. (следы), плоскости и пространства всех геометрий, включая евк­лидову, Лобачевского и Римана, описываются обра­зующим лучом, один конец которого может двигаться по линии или оставаться неподвижным, а другой, в движении, удлиняться или сокращаться. На рис. 10 показано, как, двигаясь на плоскости, образующий АО от точки А до точки А', остается неизменным по длине и описывает дугу окружности пол­ностью в соответствии с геометрией Евклида. В точке А' он в движении начинает укорачиваться и до точки А" движется по сферической кривой, описывая линию положительной кривизны в соответствии с гео­метрией Римана. В точке А" происходит следующий пе­релом и образующий на участке А" А"' начинает описы­вать линию отрицательной кривизны по геометрии Лобачевского до точки А'", после которой линия движе­ния снова меняет «свою» геометрию и т.д. Переломные точки А', А", А'", А"" имеют статическую для этой об­ласти величину луча, и потому луч может быть отнесен к геометрии Евклида. Перелом есть изменение качест­ва, процесс перехода от одной кривизны к другой.

Оба конца луча могут совершать любые движения, описывать самые различные фигуры, кроме тех, кото­рые могут привести к их пересечению между собой. Так, например, если конец луча, описывающий кривую АА'А"А'"... (рис. 10), замкнется при одновременном движении другого конца-точки О по прямой, то выпи­сывается объемная фигура — профилирован-ный ци­линдр. Если же точка О будет двигаться по окружности, то вместо цилиндра получается тор того же профиля. Таким образом, возникновение искривления как поло­жительного, так и отрицательного, связано с изменени­ем длины луча, создающего это «искривление». Длина луча, в свою очередь, зависит от напряженности про­странства в различных направлениях от точки, из кото­рой он исходит. Изменение напряженности не есть ис­кривление поверхности и не приводит к нему, а вызывает изменение метричности. И, следовательно, длины луча. Покажем это на примере (рис.11).

Пусть луч АО, исходящий из условной точки О, двигаясь по отрезку окружности АВО, начал удлиняться и в точке А' пересек прямую А"О. Продолжая дальнейшее движение, он пересек также прямую ОВ" — окончание дуги АВ.

Дуга АВ разделена прямыми на четыре равных отрезка к, l, т, п. Прямые, разделившие дугу, продолжены до пересечения эквипотенциальной линии А" В" и также делят эту дугу на четыре равных отрезка к", l", т", п". В пространстве отрезки k" = k = l′′ = l = т" = т = п" = п, как следствие пропорционального изменения напряженно­сти от точки О к периферии поверхности. Поскольку пропорциональность напряженности сохраняется на всей поверхности, то отрезок А'В' делится на четыре части к', l′, т', п′ так что: к' = l' = т' = п′ хотя по евклидо­вой и римановой геометрии к' ≠ п′.

Естественно также, что к = к' = к"; l = l' = l"; т = т' = т"; п = п' = п".

То есть все отрезки равны между собой так, что отно­шение каждого из отрезков к длине соответствующего луча между эквипотенциальными дугами будет величи­ной постоянной. Именно это свойство напряженности пространства обусловливает образование пространст­венных ячеек — основных элементов динамической гео­метрии. Напряженность и изменение метричности (кри­визна относительно статичности) — это те факторы, которые не учитывались в теории кривизны ни Гауссом, ни Риманом. Отмечу, что кривизны поверхностей, а тем более кривизны объемов в пространстве не суще­ствует. А поскольку пространство отображает динами­ческую структуру реального мира, то эмпирическое подтверждение ее адекватности этому миру можно по­лучить прямо на поверхности Земли.

Рис. 11

Приведу описание нескольких экспериментов, под­тверждающих такую возможность. В долине вблизи гор можно построить горизонтальную мерную милю из иде­ального материала длиной в 3 км (с точностью до 1 см). Произвести геодезическую съемку этой мили и перене­сти ее размеры по отвесу на горное плато на высоту одного, а лучше 2 км, и там построить другую горизон­тальную мерную милю той же длины. Современные геодезические приборы позволяют провести операцию переноса на несколько десятков километров с точно­стью до 2-3 см. В соответствии с геометрией Евклида мили и в долине и на плато должны быть разной длины. Миля на плато на высоте 1 км будет на 47 см длиннее мили в долине, а на высоте 2 км – на 94 см.

Следует замерить милю в долине несколькими мер­ными линейками, проведя ими же в аналогичных усло­виях измерение мили на плато, убедиться, что она в точности, до ошибок измерения, равна миле в долине, а, следовательно, мерные линейки изменили свою длину.

Другой эксперимент: на горе с горизонтальным плато на высоте 2 км выложить горизонтально из 40-50 сталь­ных стержней длиной по 20-25 м (± 0,1 мм) единый стержень километровой длины. Отметки его концов пе­ренести по отвесу в долину под горой, потом разобрать конструкцию, перебросить ее в долину и вновь собрать. Согласно геометрии Евклида собранная конструкция будет короче отметок на 32 см. Однако стержни при из­мерении метром окажутся в рамках отметок ± ошибка измерения.

Наконец можно просто провести геодезическими при­борами измерение отрезка относительно горизонталь­ной поверхности в долине на длине 10 км и, замерив та­кую же длину, перенесенную по отвесу на плато на высоту 2 км, убедиться с достаточно грубым приближе­нием (± 25-30 см) в исчезновении при измерении отрез­ка почти трехметровой длины. (Можно предположить, что аналогичные нестыковки уже встречались карто­графам и геодезистам и не получали теоретического объяснения.)

Рассмотрим в общих чертах структуру пространст­венной ячейки отграниченной нейтральными зонами. Пространственные первичные ячейки образуются ядра­ми по периметру своей нейтральной зоны, соизмеримые по напряженности с напряженностью окружающего пространства. Они могут включать одно ядро (редко), два ядра (большинство), несколько ядер (редко). В настоящей работе напряженность схематически обознача­ется условной линией, как бы оставляемой ядром тела, взаимодействующего с пространством. Эти линии по наглядности являются некоторым подобием фарадеевых силовых линий, а в геометрии это геодезические линии. Прямые напряженности выходят из пространства одного ядра 1(рис 12) с фиктивным центром О и входят в пространство другого ядра 2 с фиктивным центром О₂. Линии напряженности О₁АО₂, О₁ВО₂, О₁СО₂..., соеди­няющие фиктивные центры, в пространстве параллель­ны. В точках А, В, С, D,... они испытывают кажущееся преломление, обусловленное зоной единой минималь­ной напряженности — нейтральной или эквипотенциаль­ной зоной.

Ячейка образуется только тогда, когда оба ядра имеют пространственную линию общей эквипотенциальной зоны (нейтральные зоны), как бы выделяющую их из окружающего пространства. Эти зоны образует из них единую систему и не позволяет ядрам покинуть ее. Именно она обусловливает дискретность пространства одного ранга.

Первичные ячейки через нейтральные зоны взаимо­действуют с окружающими ячейками и входят в состав ячеек несоизмеримого

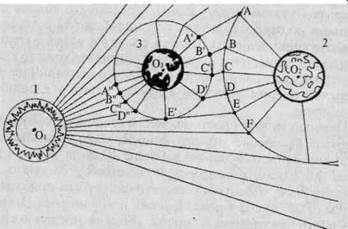
Рис. 12

ранга. Общая структура про­странства ¾ иерархия равенства. В пространстве ячей­ки между ядром и нейтральной зоной могут существо­вать спутники ядра 3с центром О₃. Между спутником и ядром также существует нейтральная зона А'В'С... А"В"С", охватывающая спутник эллиптической сферой. Выходящие из центра О₁ линии входят в центр О₃ или замыкаются в нейтральной зоне. Радиус (статический) спутника определяется граничными условиями. Про­странство ячейки, ядра и спутника всегда находятся в движении.

Ядро как элемент ячейки и самостоя­тельная система единой внутренней напряженности име­ет сложную струк­туру, обусловлен­ную материально­стью самого образо­вания. Оно включа­ет несколько «скорлуп»-сателлитов 1 (рис. 13), у которых нейтральная зона 2 каждой скорлупы находится либо вну­три этой поверхно­сти, либо у самой поверхности, что и удерживает их в единой системе. Поэтому сферы сателлитов, взаимодействуя нейтраль­ными зонами, образуют на своей внешней поверхности равновеликую напряженность, интегрированную уже как напряженность самого ядра. Пространство внутри скорлуп Рис. 13. (рис. 13) материально и имеет напряженность более высокого ранга, чем снаружи. В этом про-странст­ве может находиться внутреннее вещественное ядро-керн 3. Его напряженность несоизмерима по рангу ни с напряженностью пространства ячейки, ни с напряжен­ностью сателлитов. Она есть плотность другого ранга.

Геометрия свойств здесь о свойствах как элементах геометрии

2.3. Свойства пространственных систем

Рассмотрим, что неявно происходит с пространством при возникновении в нем тел, отображаемых элемента­ми динамической геометрии [28]. Возьмем чистый лист бумаги и предположим, что этот лист есть некоторая плоскость, однородная и изотропная в четырех направле­ниях, а, следовательно, на пространстве листа мы не за­мечаем никакой структуры и внутренней напряженно­сти. Эта поверхность может быть названа бес­форменной, хаотичной, или поверхностью одного ранга. Структура этого ранга и его ячейки нами не фиксируют­ся.

Поставим в любом месте листа точку. Точка на листе никакой роли не играет, структуры не создает, и как бы не возникает напряженности различной плотности на всей поверхности. Но хаос уже исчез, точка изменяет качество всего пространства и становится центром образования нового пространства, центром структуризации и изменения его качеств, центром дру­гого ранга. И не существенно, пространство ли это лис­та или пространство космоса, в котором имеется тело. Существенно в подходе к явлению, к его формализации ¾ другое. Образует ли точка пространство актуальной бесконечности или бесконечности потенциальной? Именно одна из сторон двойственности обусловливает процесс понимания формализации элементов различных пространств по мере их воссоздания на листе.

Точка, как и другие элементы в пространстве потен­циальной бесконечности (или в объеме), не равнозначна другим не видимым на листе точкам и уже создает (да­же если это не отражают условия задачи) в окружающем пространстве некоторую напряженность, определяемую изменением метрического пространства. Именно метричность есть агент, отображающий распространение плотности напряженности от точки в пространстве. При этом на бесконечности одного ранга плотность убывает от точки до нуля. (Нулевая плотность напряженности равна напряженности, создаваемой телами нижнего ран­га и потому не равна 0.) Поскольку значимость точки определяется ее рангом и рангом пространства, то ранги определяют также изменение метричности.

Если на плоскости (в пространстве) имеется две или несколько точек, то напряженность между ними опре­деляется рангом точек. Поскольку в задачах чаще всего задается одинаковый ранг, то плотность напряженности между точками становится неоднозначной. Но между ними всегда имеется зона одинаковой плотности напря­женности — нейтральная зона. Структура всех напря-женностей между точками определяется именно харак­тером и местом нейтральных зон. В плоскости (как и в объеме) актуальной бесконечности напряженность от­сутствует, а следовательно, может отсутствовать и метричность (что и наблюдается в проективной геометрии). Если же она присутствует, то неизменна величиной по всей плоскости (по всему объему), и точка, как и другие фигуры в этом пространстве, на пространство никакого влияния не оказывает.

Поставим еще одну точку. Структуризация возросла и снова изменилось качество всего пространства. Между точками по различным критериям может быть найдена активная область или нейтральная зона, разде­ляющая как их, так и плоскость листа. Или они могут быть соединены одной линией, которая делит лист уже на две иные, чем нейтральная линия, части, создавая иные пространства по обе ее стороны.

Соединим точки линией, и в одном из образовавшихся пространств в стороне от линии поставим точку, создав тем самым все необходимые предпосылки для форму­лирования или пятой аксиомы Евклида или основной аксиомы динамики пространства. Все имеющиеся на плоскости элементы равнозначны или, по современной артикуляции, равноправны, и только движение опреде­ляет их принадлежность к динамике. Если теперь со стороны прямой, восстановив до точки М образующий луч, двигать его неизменным по длине вдоль прямой, то точка, в которую он вошел, будет оставлять след евкли­довой прямой, параллельной базовой. И это будет про­должаться бесконечно, если... если мы не последуем за Дезаргом. Дезарг, исходя из кажущегося пересечения в перспективе параллельных в одной точке, предложил считать пересечения проекциями «бесконечно удален­ных» точек, равноправными со всеми остальными эле­ментами. Так, в проективную геометрию вошли «несоб­ственные (бесконечно удаленные) точки» и «несобст­венные плоскости» — плоскости, на которых лежат эти точки.

Введение «несобственных» точек и плоскостей нарушило равнозначность элементов геометрии, было пер­вым качественным отображением на плоскости фак­торов напряженности пространства и свидетель­ствовало о другом ранге несобственных точек. Однако нарушения равнозначности элементов обнаружено не было, и не потому, что оно отсутствует, а потому, что и обычным, и несобственным точкам и площадям постулировали равноправие. Это постулирование рав­ноправия обусловило полную статичность проективной геометрии, нивелировало напряжен-ности, привело к тому, что все прямые одной плоскости Дезарга всегда пересекаются на бесконечности. Таким образом, во­прос о различной напряженности у точек и линий на плоскости даже не возник. Развитие получили аксиомы статической геометрии.

Если теперь, для примера, представить движение колес паровоза по рельсам в пространстве обычном и не­собственном (потенциальной бесконечности), то мы увидим, как бы следуя за ним неизменными, что рельсы сначала будут параллельными (расстояние между ними — образующий луч, остается неизменным). Затем под воздействи­ем возрастающей напряженности несобственного про­странства начнут сходиться (образующий луч будет уменьшаться и, соответственно, паровоз тоже), и, по­дойдя к несобственной точке, луч станет по «длине» меньше ее. Пройдя поверхность сферы-точки, т.е. про­никнув в объем другого ранга, луч продолжает умень­шаться и, миновав центр (но не через него), начинает возрастать до противоположной поверхности сферы.

Поскольку напряженность поверхности вокруг точки сферически симметрична (в предположении, что точка находится вдали от других точек), по выходу из несоб­ственной точки луч начнет расширяться, а рельсы, сле­довательно, расходиться под тем же самым углом, под которым они сходились. В результате возникнет полная иллюзия того, что в несобственной точке произошло пе­ресечение рельсов. На самом деле, на всем протяжении движения к точке, сквозь нее и за ней рельсы оставались параллельными. Менялась же напряженность несобст­венного пространства и несобственной точки в полном соответствии с динамикой пространства, что и создава­ло иллюзию схождения и расхождения рельсов. (Иллюзию их пе­ресечения в одной точке.)

Дата добавления: 2015-07-11