
Читайте также:
|
Передаточною функцією (ПФ) називається відношення зображення за Лапласом вихідної величини Y(p) до зображення за Лапласом вхідної величини X(p) при нульових початкових умовах:
W(p) =  =
= 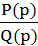 ,
,
де поліном Q(p) називають характеристичним, P(p) - оператором впливу, а рівняння виду Q(p)=0 називаютьхарактеристичним рівнянням.
Перш, ніж приступити до визначення передаточних функцій елементів САР, необхідно перейти від диференціальної форми рівняння до алгебраїчної. Даний перехід базується на, так званому, перетворенні Лапласа, що пов'язує змінну величину x(t) у функції часу t зі змінною величиною x(p) у функції комплексного змінного p:
x(р) =  x(t)e-ptdt,
x(t)e-ptdt,
x(t) = 
 x(p)eptdp,
x(p)eptdp,
де x(t) – оригінал функції x(p);
x(p) – зображення функції x(t) за Лапласом;
p – оператор Лапласа.
Перехід від функції x(t) до її зображення x(p) називається прямим перетворенням Лапласа, а перехід від зображення x(p) до оригіналу x(t) – зворотнім перетворенням Лапласа.
Практичний перехід від диференціального рівняння до алгебраїчного, для рівнянь поліноміального виду, виконують без будь-яких обчислень, лише формальною заміною dn / dtnна pnі функції x(t) і y(t) - їх зображеннями x(p) та y(p).
Розглянемо перехід від диференціального рівняння до ПФ на прикладі об'єкту керування.
Диференціальне рівняння об’єкту керування (серверной)
25000  + 2900
+ 2900  + 𝜣 t = 0,015g(t)
+ 𝜣 t = 0,015g(t)
Зробимо перехід від диференціального рівняння до алгебраїчного, замінивши похідні на оператор Лапласа p
(25000p2 + 2900p +1) 𝜣 (p) = 0,015g(p)
де 1500p +100p+1 - характеристичний поліном ланки (сервернії) - Q(p);
0,5 – коефіцієнт підсилення ланки (серверній);
Q(p) – вихідний сигнал за Лапласом – Y(p);
g(p) – вхідний сигнал за Лапласом – X(p).
За формулою визначимо передаточну функцію об’єкту керування Wокв операторній формі
Wок(p) = 
Аналогічно визначимо передаточні функції для інших ланок САР:
Wд(p) = 
Wрег(р) = 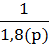
Wве(р) = 0,1
Дата добавления: 2015-07-11; просмотров: 119 | Нарушение авторских прав