Задача 3. Проектный расчёт ступенчатого бруса

Для стального ступенчатого бруса (рис. 1.6, а) задана конфигурация и известна внешняя нагрузка.

Требуется:

1. Построить эпюру продольных сил .

2. Составить выражения для нормальных напряжений 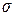по всем участкам бруса, используя указанные на схеме бруса значения площадей сечения через неизвестную величину .

3. Установить 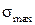, составить условие прочности бруса по допускаемым напряжениям. Найти из этого условия требуемое значение при 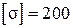МПа и назначить площади всех участков бруса, соблюдая указанное соотношение между ними.

4. Построить эпюры нормальных напряжений и продольных перемещений 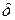, считая модуль упругости 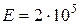МПа. Указать 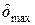и проверить жёсткость при допускаемом продольном перемещении 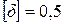мм. Если условие жёсткости не удовлетворяется, назначить новые площади сечений.

5. Для опасного сечения бруса вычислить касательные 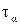и нормальные напряжения в наклонной площадке, проведённой под углом 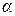=45° к оси бруса.

6. Какую силу 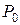нужно приложить к свободному торцу бруса, чтобы вернуть его в первоначальное положение?

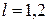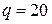Исходные значения: м; кН/м; .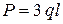

Решение

1. Построим эпюру продольных сил .

Вычислим значения продольных силметодом сечений. Данный брус состоит из 3-х участков. Будем рассматривать отсечённые участки для каждого участка, начиная со свободного конца (рис. 1.6, б, в, г). При этом продольную силу в сечении, которая является внутренним усилием, всегда изображаем положительной, т.е. растягивающей рассматриваемый участок.

Уравнение равновесия для отсечённой части каждого участка при растяжении-сжатии представляет собой равенство нулю суммы проекций всех сил на продольную ось (1.1), т. е. .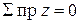

Записывая это уравнение последовательно для всех участков получим продольные силы для каждого участка:

;

.

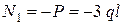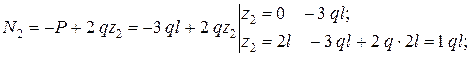
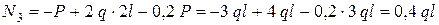По этим значениям построим эпюру (рис. 1.6, д).

2. Выражения для нормальных напряжений

Составим выражения для нормальных напряжений 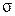по всем участкам бруса, используя указанные на схеме бруса значения площадей сечения через неизвестную величину .

а б в г д е ж

Рис. 1.6

Нормальное напряжение вычисляем для каждого участка бруса по формуле (1.3) как

.

Получаем ;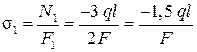

.

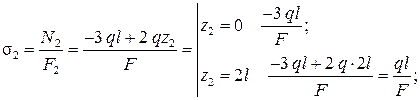
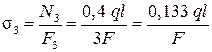3. Нахождение 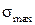и условие прочности

Условие прочности ступенчатого бруса при растяжении-сжатии по допускаемым нормальным напряжениям имеет вид (1.5), согласно которому

. (1.15)

Значит, нужно выбрать из полученных значений нормальных напряжений 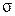наибольшее по модулю значение, здесь имеем

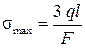. Тогда по (по1.15) получаем .

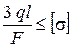Из этого условия вычислим требуемое значение и назначим площади всех участков бруса, соблюдая указанное соотношение между ними.

.

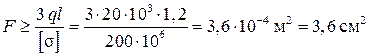Принимаем 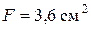. Назначим площади всех участков бруса, соблюдая указанные на схеме бруса соотношения между ними:

, , .

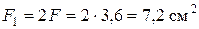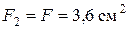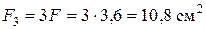4. Э пюры нормальных напряжений и продольных перемещений.

Вычислим значения нормальных напряжений по участкам бруса, используя полученные выше выражения.

;

.

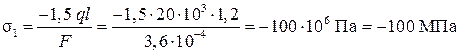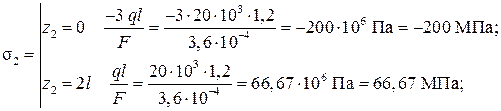
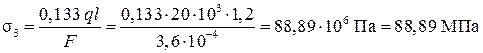Откладывая полученные значения от базисной линии, построим эпюру распределения нормальных напряжений по длине балки (эпюру 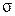) (рис. 1.6, е).

Построим эпюры продольных перемещений .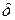

Перемещения 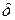поперечных сечений бруса вычисляют по (1.7) через продольные деформации участков бруса 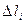.Сначала найдём деформации 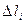участков бруса.

Согласно формуле (1.6) ,

где 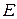– модуль упругости первого рода или модуль Юнга; – площадь поперечного сечения; 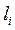– длина участка бруса. Заметим, что в случае постоянной по участку продольной силы имеем .

.

.

.

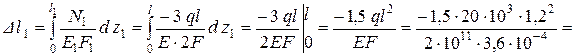
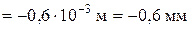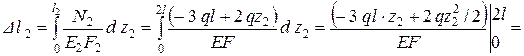
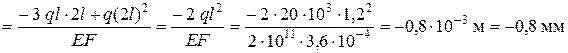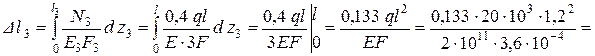
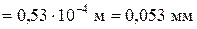Теперь определим продольные перемещения δ_i характерных сечений, обозначив сечения буквами , , , . Так как точка находится в заделке, то перемещение 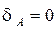; Перемещения сечений , , определяем с помощью (1.7):

;

;

.

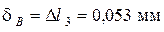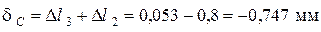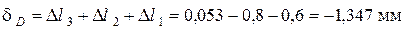На участке 2 эпюра продольных сил пересекает нулевую линию в точке 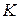(рис. 1.6, д), в этом сечении будет перегиб на эпюре перемещений, поэтому определим координату 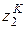из условия :

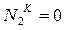получаем 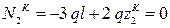; отсюда .

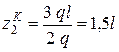Вычислим продольную деформацию участка CK:

.

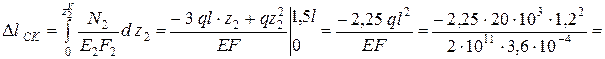
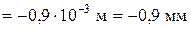Тогда продольное перемещение сечения K согласно (1.7) равно

.

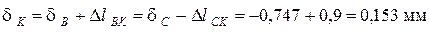По полученным значениям построим эпюру продольных перемещений (рис. 1.6, ж).

Укажем 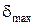и проверим жёсткость при допускаемом продольном перемещении.

Используем условие жёсткости (1.9), для которого выбираем из полученных значений наибольшее по модулю: 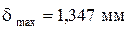. Тогда условие жёсткости принимает вид

.

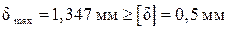Как видим, условие жёсткости не выполняется. Необходимо назначить новые площади сечений, чтобы соблюдалось условие жёсткости, которое в нашем примере должно иметь вид

.

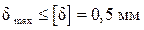Запишем 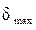через нагрузку и жёсткость сечения :

.

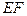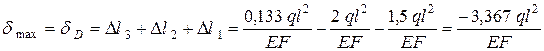Тогда условие жёсткости получает выражение

.

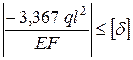Откуда .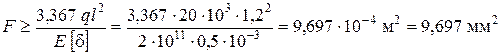

Принимаем 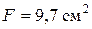и окончательно назначаем площади участков бруса:

, , .

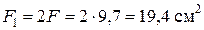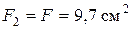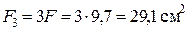5. Касательные и нормальные напряжения в наклонной площадке

Для опасного сечения бруса вычислим касательные 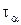и нормальные 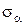напряжения в наклонной площадке, проведённой под углом 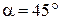к оси бруса.

Напряжения подсчитаем по формулам (1.10), подставляя значения нормальных напряжений в опасном сечении C:

;

.

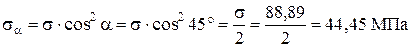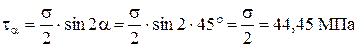6. Определение силы

Определим, какую силу нужно приложить к свободному торцу бруса, чтобы вернуть его в первоначальное положение. Сечение Д получило отрицательное перемещение 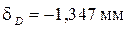. Чтобы вернуть сечение в первоначальное положение, нужно, очевидно, приложить растягивающую силу Р ₀, которая растянет брус на 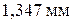, т. е. деформация всего бруса от силы Р ₀ составляет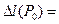 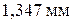. Записывая эту деформацию как сумму деформаций участков, получим уравнение

.

.

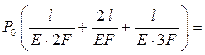
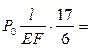
Отсюда 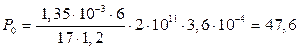кН.

Дата добавления: 2015-07-11