Читайте также:
|
Стальной ступенчатый брус (рис. 1.7, а) жёстко закреплён с торцов. Задана конфигурация бруса и известна внешняя нагрузка: 
м; 
; 
кН/м.
Требуется:
1. Используя условие равновесия и уравнение перемещений, найти величины реактивных сил, возникающих в жёстких заделках.
2. Построить эпюру продольных сил N.
3. Составить выражения для нормальных напряжений s по всем участкам бруса, используя указанные на чертеже бруса значения площадей сечения через неизвестную величину F.
4. Установить smax., составить условие прочности бруса по допускаемым напряжениям. Найти из этого условия требуемое значение F при [s]=200МПа и назначить площади всех участков бруса, соблюдая указанное соотношение между ними.
5. Построить эпюры нормальных напряжений sи продольных перемещений δ, считая модуль упругости E =2∙105МПа. Указать δmax и проверить жёсткость при допускаемом продольном перемещении [δ] = 0,5 мм. Если условие жёсткости не удовлетворяется, назначить новые площади сечений.
6. Для опасного сечения бруса вычислить касательныеτα и нормальные sα напряжения в наклонной площадке, проведённой под углом α = 45° к оси бруса.
7. Вычислить температурные напряжения, возникающие при повышении температуры среды на 40°. Принять коэффициент линейного удлиненияa = 1,25∙10-5 1/град.
8. Как изменятся величины реактивных сил, если между правой заделкой и торцом бруса будет зазор величиной 0,0001∙ L?
Решение:
1. Вычисление реактивных сил
Обозначим реактивные силы, возникающие в жёстких заделках под нагрузкой, как 
и 
(рис. 1.7, а). Их величины должны удовлетворять уравнению равновесия всего бруса при растяжении-сжатии (1.1), т. е. 
, которое принимает вид
. (1.16)
Как видно, это уравнение содержит два неизвестных и 
, поэтому брус является статически неопределимым. Для нахождения и необходимо составить еще одно уравнение – уравнение перемещений.
При растяжении-сжатии ступенчатого бруса уравнение перемещений записывают через продольные деформации участков 
. Данный брус состоит из трёх участков, поэтому
, (1.17)
| а б в г д е ж | 
|
Рис. 1.7
где выражения деформаций участков бруса 
, 
и 
составляем по (1.6) как 
, где 
– продольное усилие на рассматриваемом участке; где 
– модуль упругости первого рода или модуль Юнга; 
– площадь поперечного сечения;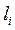 
– длина участка бруса. Заметим, что в случае постоянной по участку продольной силы имеем 
.
Сначала запишем для каждого участка бруса продольные усилия и абсолютные деформации. Продольные силыопределяем методом сечений, рассматривая отсечённые части каждого участка (рис. 1.7, б, в, г), начиная со свободного конца. При этом продольную силу изображаем положительной, т.е. растягивающей рассматриваемый участок.
Используя уравнение равновесия отсечённой части 
, записываем последовательно продольные силы для каждого участка:
; 
; 
;
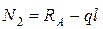Составим выражения деформаций участков бруса 
, и , причём площади сечения возьмём по конфигурации бруса через неизвестное значение F:
;
;
.
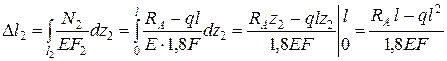Подставляя в (1.17) эти величины, получим уравнение перемещений, записанное через :
. (1.18)
Уравнение равновесия (1.16) и уравнение перемещений (1.18) составляют систему 2-х урвнений с двумя неизвестными и , решая эту систему найдём величины этих реактивных сил. Уравнение (1.18) есть уравнение с одним неизвестным . Тогда, умножая его на EF, получаем
,
,
.
Из уравнения (1.16) 
.
2. Построим эпюру продольных сил N.
Подставив найденную реакцию в выражения продольных усилий по участкам, получим их значения:
Откладывая от базисной линии эти значения, построим эпюру 
(рис. 1.7, в).
3. Выражения нормальных напряжений
Составим выражения нормальных напряжений 
для каждого участка вала по формуле (1.3) как 
:
;
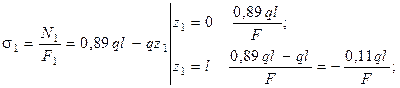
4. Условие прочности бруса
Условие прочности ступенчатого бруса при растяжении-сжатии по допускаемым нормальным напряжениям запишем по (1.5):
.
Выбираем smax из полученных выше значений нормальных напряжений 
как наибольшее по модулю,
,
Теперь условие прочности получаем в виде
.
Найдём из этого условия требуемое значение 
и назначим площади всех участков бруса, соблюдая указанное соотношение между ними.
.
Принимаем 
и назначаем площади всех участков бруса:
, 
.
5. Э пюры нормальных напряжений и продольных перемещений
Вычислим значения нормальных напряжений по участкам бруса, используя полученные выше выражения.
Откладывая полученные значения от базисной линии, построим эпюру распределения нормальных напряжений по длине балки (эпюру ) (рис. 1.7, е).
Построим эпюры продольных перемещений 
.
Сначала подставляем в полученные ранее выражения деформаций участков бруса найденные величины площадей и получаем значения деформаций.
;
;
.
Определим продольные перемещения характерных сечений, обозначив сечения буквами 
, 
, 
, D.
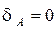, т.к. точка находится в заделке; перемещения сечений , , 
определяем с помощью (1.7):
;
Продольное перемещение в сечении D оказался равным нулю, т.к. это сечение находится в заделке.
По полученным значениям построим эпюры продольных перемещений (рис. 1.7, ж). Уточним линию на первом участке, где имеем линейный характер силы N 1и пересечение её эпюры с базисной линией в сечении K при 
:
.
Вычислим координату 
. Перемещение этого сечения равно деформации участка AK, поэтому
.
Отложив это значение, проводим кривую с перегибом в точке K.
Проверим условие жёсткости, для этого из эпюры перемещений возьмём 
и запишем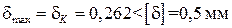 
, значит условие жёсткости выполняется.
6. Касательные и нормальные напряжения в наклонной площадке
Для опасного сечения бруса вычислим касательные τα и нормальные sα напряжения в наклонной площадке, проведённой под углом α = 45° к оси бруса. Напряжения на наклонных площадках вычисляют по известным формулам (1.10):
, 
.
7. Температурные напряжения
Вычислим температурные напряжения, возникающие при повышении температуры среды на 40°. Для этого составим уравнение перемещений (1.17), учитывая удлинение от температуры и сжатие от реакций, возникающих в заделках. При этом удлинение определяем по формуле
.
,
или 
.
Отсюда
Вычислим наибольшие температурные напряжения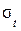 
, которые будут возникать в более тонком месте − на 1-м участке:
8. Влияние зазора на величину реакций
В случае зазора при действии температуры торец бруса переместиться за счёт деформации на величину зазора. Поэтому величины реактивных сил должны удовлетворять уравнению перемещений, в котором правая часть равна 0,0001∙ L 1:
.
Как видим, значение температурных реакций при наличии зазора уменьшается.
Дата добавления: 2015-07-11; просмотров: 518 | Нарушение авторских прав