Задача 2. Подбор размеров сечения стержней фермы

Для плоской фермы (рис. 1.5, а) задана нагрузка. Исходные значения: м; кН/м; ; .

Требуется:

1. С помощью уравнений равновесия определить опорные реакции.

2. Используя метод вырезания узлов, определить усилия в стержнях фермы.

3. Подобрать размеры поперечного сечения стержней из условия прочности по допускаемым напряжениям, если допускаемые напряжения МПа. Сечение сжатых стержней принять в форме кольца с соотношением внутреннего и внешнего диаметров равным 0,5, а сечении растянутых стержней – в виде швеллера.

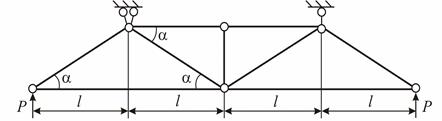
а
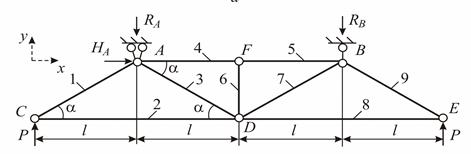
б
в	г	д

Рис. 1.5

Решение

1. Определение опорных реакций

Обозначим реакции, возникающие в опорах и . Опора шарнирно-подвижная, имеем один вертикальный опорный стержень, вдоль которого возникает одна вертикальная реакция (см. замечание 1) (рис. 1.5, б). Опора шарнирно-неподвижная, она препятствует смещению узла по вертикали и горизонтали, поэтому в ней в общем случае возникает две реакции: горизонтальная и вертикальная , но поскольку в горизонтальном направлении нет других сил, то из уравнения следует, что .

Ферма нагружена системой параллельных сил , и . Составим два уравнения равновесия:

Запишем эти уравнения:

Из (1.12) кН.

Из (1.13) кН.

Проверку найденных рекций выполним по неиспользованному уравнению, которое при правильном вычислении реакций удовлетворяется тождественно, : ;

;

; ,

значит, реакции найдены верно.

Равенство есть следствие симметрии фермы, поэтому можно сформулировать следующее.

Замечание 4: в симметричной схеме при симметричной нагрузке реакции равны друг другу, а величина их составляет половину нагрузки.

2. Определение усилий в стержнях фермы

Обозначим узлы и пронумеруем стержни (рис. 1.5, б). В стержнях ферм, которые имеют по концам шарниры, возникают только продольные силы (см. замечание 1). Их значение определим методом вырезания узлов, который основан на методе сечений. По этому методу последовательно вырезаем каждый узел фермы и рассматриваем его равновесие. В данной ферме в силу её симметрии необходимо и достаточно выделить три узла: узлы , , .

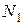Первым вырезаем узел (рис. 1.5, в), в котором сходятся два стержня: 1 и 2. Продольные усилия в стержнях и 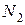направляем от сечения, предполагая растяжение. Для этого, как и для каждого узла имеем сходящуюся систему сил, поэтому составляем два уравнения равновесия, из которых и найдём неизвестные усилия,

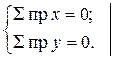
Запишем эти уравнения для узла

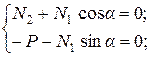или

Из полученных урвнений вычислим усилия и :

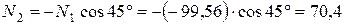кН,

кН.

Продольное усилие 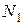отрицательно, значит, стержень 1 сжат. Продольное усилие 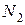положительно, поэтому стержень 2 растянут.

Следующим нужно рассматривать узел, в котором неизвестны два продольных усилия; в нашем примере вырезаем узел (рис. 1.5, г), в котором неизвестны усилия в стержнях 3 и 4. Ставим усилия в стержнях 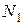, , и реакцию . Составляем уравнения равновесия узла по :

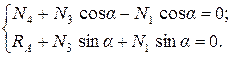
Подставив уже найденное значение 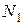, получим систему двух уравнений относительно неизвестных и :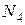

Отсюда

,

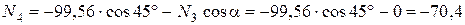кН.

Стержень 3 не растягивается и не сжимается, поскольку продольное усилие в нём равно нулю. Т.к. продольное усилие 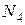отрицательно, то стержень 4 сжат.

Сдедующим вырезаем узел (рис. 1.5, д), для которого уравнения равновесия по будут

Или

Получаем и 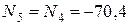кН. Стержень 6 не деформируется, поскольку продольное усилие в нём равно нулю. Усилие отрицательно, это означает, что стержень 5 сжат.

Поскольку конструкция симметричная, то достаточно рассмотреть лишь одну её половину и можно записать внутренние усилия в симметричных стержнях второй половины,т. е. усилия попарно равны

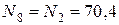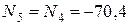кН; кН;

кН; кН.

3. Подбор размеров сечения стержней

Размеры поперечного сечения стержней подбираем из условия прочности по допускаемым напряжениям, которое при растяжении-сжатии по (1.4) имеет вид

,

где – нормальное напряжение в стержне; 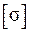– допускаемые нормальное напряжение, здесь при растяжении и сжатии они одинаковы; – продольное усилие в стержне; – поперечное сечение стержня.

Для растянутых стержней нужно выбирать номер швеллера. Если нет дополнительных условий, считаем все растянутые стержни одинакового сечения. Максимальные растягивающие усилия кН, тогда из условия прочности требуемая площадь сечения растянутых стержней

.

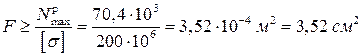По таблице ГОСТ 8240-93 (табл.5 Приложения) выбираем швеллер № 5 с площадью для стержней 2 и 8.

Для сжатых стержней выбираем кольцевое сечение, для которого площадь . Считая все сжатые стержни одинаковой площади и взяв максимальное сжимающее усилие 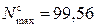кН, найдём требуемую площадь сечения как

.

Тогда диаметр поперечного сечения сжатых стержней

.

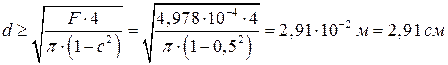Принимаем диаметр для стержней 1, 4, 5, 9.

Стержни, в которых 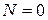, можно принять также круглого сечения, поэтому для стержней 3, 6, 7 принимаем диаметр .

Дата добавления: 2015-07-11