Раздел 1. РасчЁты при растяжении-сжатии

В этом разделе рассматриваются расчёты на прочность и жёсткость при растяжении и сжатии. Растяжение и сжатие возникает: в опорных стержнях, поддерживающих какие либо конструкции (сооружения, плоские и пространственные рамы, ─ в целом эти системы называют стержневыми системами); в стержнях ферм (фермы − это системы из прямолинейных стержней, соединённых по концам шарнирами); в элементах конструкций, имеющих вид прямого бруса постоянного или переменного сечения и нагруженных продольной нагрузкой. Например, как прямой брус при действии растягивающей силы рассматривают болты и винты, применяемые в механических соединениях; трос подъёмного механизма; как прямой брус изображают следующие элементы, воспринимающие продольную нагрузку: колонны зданий и оборудования, фабричные трубы, столбчатые фундаменты, которые сжаты собственном весом и верхней нагрузкой.

При составлении схем расчёта при растяжении и сжатии учитываются геометрия всей системы, вид внешнего воздействия, и способ присоединения (или опирания). Если присоединение фактически препятствует смещению и повороту, то на схеме изображается так называемая жёсткая заделка. Если опора не позволяет линейного перемещения, а поворот частей системы относительно друг друга происходит, то такое соединение называют шарнирным и на расчётной схеме изображается шарнир.

По количеству имеющихся опор схемы для расчёта могут быть как статически определимыми (количество опорных связей равно количеству уравнений равновесия), так и статически неопределимыми (количество опорных связей превышает количество уравнений равновесия). Ввиду этого в данном пособии рассматривается решение следующих задач, которые задают в курсовой работе и в расчётно-графических заданиях по сопротивлению материалов.

Задача 1. Подбор размеров сечения стержней стержневой системы.

Задача 2. Подбор размеров сечения стержней фермы.

Задача 3. Проектный расчёт ступенчатого бруса.

Задача 4. Проектный расчёт ступенчатого статически неопределимого бруса.

Задача 5. Проектный расчёт стержневой статически неопределимой системы.

Задача 6. Проверочный расчёт ступенчатого бруса.

Задача 7. Проверочный расчёт ступенчатого статически неопределимого бруса.

В каждой из названных задач необходимо выполнить расчёт на прочность, в ходе которого всегда требуется знать значение внутренней продольной силы N, так как в случае растяжения и сжатия в поперечных сечениях бруса возникают только продольные силы, которые и позволяют оценить сопротивление бруса внешним воздействиям.

Известно, что в общем случае нагружения в поперечном сечении бруса могут возникать шесть разных внутренних усилий, но при решении задач изображают и вычисляют только те усилия, которые не равны 0. Так, при растяжении и сжатии по виду внешних сил видно, что в сечении возникает лишь продольная сила N.

Выполним вычисление продольной силы N на примере бруса с нагрузкой общего вида: в начальном сечении бруса покажем сосредоточенную силу Р ипо всей длине распределённую нагрузку интенсивности q (рис. 1.1, а).Введём правило знаков нагрузки: принимаем за положительное то направления, которое вызывает растяжение.

а
б
в
г

Рис. 1.1

Значения продольной силы вычисляют методом сечений, выполняя последовательно правило РОЗУ: Р азрезать, О тбросить, З аменить, У равновесить. Выполним разрез бруса на расстоянии z от свободного края (это будет текущее сечение) и изобразим правую часть (рис. 1.1, б). В текущем сечении поставим силу N. Если изобразить силу N от сечения, то она растягивает отсечённую часть бруса. Такое направление продольной силы принято считать положительным. Заметим, что, поставив силу N в текущем сечении, мы произвели замену воздействия отброшенной части бруса на оставленную. Составим уравнение равновесия. Как известно, для пространственного тела имеем шесть уравнений равновесия, но при растяжении-сжатии из шести уравнений равновесия только одно не превращается в тождество 0=0, − это сумма проекций всех сил на продольную ось бруса:

Σ пр z =0. (1.1)

В нашем примере в это уравнение войдут внешние силы и и внутренняя продольная сила N, и уравнение принимает вид: отсюда получим формулу продольной силы

. (1.2)

Как видно, продольная сила N в сечении равна алгебраической сумме проекций на ось z всех внешних сил, действующих по одну сторону от рассматриваемого сечения. Получается закономерность: положительная внешняя нагрузка создаёт положительную продольную силу.

Принято изображать график изменения N вдоль оси, который называют эпюрой N. Этот график удобен, так как наглядно показывает изменение силы вдоль бруса и определяет опасное сечение: опасным является сечение, в котором продольная сила принимает максимальное значение (определяется максимальная растягивающая и максимальная сжимающая силы). Эти значения являются расчётными значениями силы и необходимы для составления условия прочности.

Для построения эпюры N вычислим значения силы в начале бруса (при z = 0) и в конце (при z = l). Получим граничные значения продольной силы: Отложив эти значения от базисной (нулевой) линии, проведённой под брусом, соединим значения согласно с (1.2) наклонной прямой и получим эпюру N. При положительных значениях нагрузки, показанной на чертеже бруса, она выглядит нарастающей от свободного края по линейному закону (рис. 1.1, в). Реальная нагрузка вносит свои коррективы: подставляя значения реальной нагрузки в формулу (1.2), можно получить функцию продольной силы и построить эпюру N для любого грузового участка расматриваемого бруса. С другой стороны, формула (1.2) позволяет проследить закономерности функции N, связанные с видом и направлением внешней нагрузки:

· на участке, где интенсивность распределённой нагрузки , продольная , и на эпюре N – прямая, параллельная оси;

· на участке с распределённой нагрузкой, где q ≠0, продольная N изменяется линейно, и на эпюре N – наклонная прямая, причём при q >0 продольная сила растёт, при q < 0 продольная сила уменьшается.

Заметим следующие методические приёмы при нахождении силы N:

1. Силу N в сечении лучше предполагать положительной (т. е. направленной от сечения). Это удобно, так как получив её значение, автоматически указывается знак «+» при растяжении и знак «–» при сжатии, что особенно важно при расчёте бруса из материала, не одинаково работающего на растяжение и сжатие.

2. Определение продольной силы для бруса с заделкой удобно выполнять, рассматривая отсечённую часть со стороны свободного края, так как приэтом не обязательно определение опорных реакций.

Расчёт элементов деталей машин и механизмов ведётся в пределах упругих деформаций, поэтому используют условие прочности по допускаемым напряжениям, общий вид которого имеет вид . Согласно этому условию напряжения не должны превышать допускаемого напряжения . При растяжении-сжатии нормальные напряжения в поперечном сечении бруса σ равномерно распределены по площади (см. рис. 1.2) и определяются как отношение продольной силы к площади сечения:

. (1.3)

В рассматриваемых ниже задачах имеются, во-первых,стержни, в которых площадь сечения F и продольная сила вдоль оси постоянны, и, во-вторых, ступенчатый брус, имеющий несколько грузовых участков с разной площадью сечения F и различным характером нагрузки. Для первых стержней условие прочности по допускаемым напряжениям записываем как

, (1.4)

а для ступенчатого бруса условие прочности принимает вид

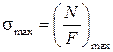
. (1.5)

Нужно помнить, что для пластичных материалов (например, для малоуглеродистых низколегированных сталей) имеем одинаковые допускаемые напряжения на растяжение и сжатие, т. е. = = , а для хрупких материалов (например, для чугуна) допускаемые напряжения на растяжение и на сжатие различны. Поэтому для пластичных материалов составляем одно условие прочности, а для хрупких − два условия.

По условию прочности возможно выполнение трёх видов расчёта на прочность:

· проектный расчёт (это определение размеров сечения);

· проверочный расчёт (вычисление напряжений и проверка прочности);

· определение несущей способности (нахождение величины нагрузки).

В рассматриваемых ниже задачах рассмотрены два первых вида расчёта.

При работе реальных систем длина стержня или его части изменяется, что вносит свои особенности в обслуживание и сохранение работоспособности всей системы, поэтому в задачах предусмотрено вычисление деформаций и проверка жёсткости. Величина изменения длины стержня (рис.1.2, а), называемая абсолютной деформацией Δ l, вычисляется как

, (1.6)

где E – модуль продольной упругости (или модуль Юнга), для стали и чугуна Е= 2∙10⁵МПа, для алюминиевых сплавов Е= 0,65 10⁵МПа; величина EF называется жёсткостью сечения при растяжении-сжатии.

За счёт деформации стержня происходит поступательное перемещение δпоперечных сечений стержня в продольном направлении. Поясним вычисление перемещений δ на нашем примере (рис. 1.1, г). Перемещение заделки δ _А равно 0, т. е. δ _А =0, а свободный край бруса переместился на величину деформации всего бруса, которую найдём по (1.6):

.

Здесь выражение, полученное после интегрирования, показывает, что имеем функцию 2-го порядка по отношению переменной z (это результат действия распределённой нагрузки), значит, величина перемещения текущего сечения, задаваемого абсциссой z, изменяется вдоль бруса по квадратичной зависимости от z, ─ по квадратичной параболе.

При расчёте ступенчатого бруса для вычисления перемещений отдельных (так называемых характерных) сечений необходимо знать абсолютные деформации грузовых участков бруса, определяемые формулой (1.6). При этом перемещение i -го сечения будет равно перемещению (i -1)-го плюс деформация i -го участка:

. (1.7)

Используя полученные значения перемещений, строят эпюруδ, которая наглядно показывает изменение продольных перемещений вдоль бруса и позволяет выбрать его наибольшее значение δ_max. Для бруса, изображённого на рис. 1.1, эпюраδ будет криволинейной, для которой нужно правильно изобразить форму кривой. Для определения угла наклона касательной к кривой перемещений, возьмём производную от функции перемещений (1.7), с учётом (1.6) получим

. (1.8)

Как видно, угол наклона касательной к кривой перемещений повторяет закон изменения силы N, поэтому эпюра N всегда позволяет определить наклон кривой δ: так в рассматриваемом примере сила N растёт от свободного края к заделке, поэтому угол наклона касательной увеличивается к заделке, и выпуклость обращена вверх (рис. 1.1, г).

Нужно заметить, что согласно с (1.8), функция перемещений δ(z) на порядок выше функции N (z):

· на участке бруса, где N= const иэпюра N – прямая, параллельная оси, на эпюре перемещений δ будет наклонная прямая;

· там, где на эпюре N – наклонная прямая, на эпюре перемещений δ ─ кривая 2-го порядка (парабола), изогнутость которой и определяется согласно (1.8) по значениям силы N.

Для обеспечения нормальной работы конструкции необходимо, чтобы значение δ_max не превышало допускаемого перемещения , в таком случае говорят, чтобы выполнялось условие жёсткости, которое имеет вид:

. (1.9)

Это условие позволяет выполнять те же три вида расчётов, что и условие прочности. Поэтому, когда оно для рассматриваемого элемента не соблюдается, по нему определяют требуемые величины.

Для правильного контроля работы конструкций надо знать, какие напряжения возникают не только в осевом направлении, но и на любом наклонном к оси. Если стержень разрезать двумя поскостями (рис. 1.2, а): плоскостью 1-1, перпендикулярной оси и плоскостью 2-2, наклонённой к поперечному сечению под углом , далее выделить полученную часть стержня (рис. 1.2, б) и рассмотреть её равновесие по уравнению (1.1), − то получим в наклонном сечении напряжения , параллельные σ и равные . Разложим вектор напряжения на нормаль и касательную к наклонному сечению и получим, что при растяжении-сжатии в наклонных сечениях возникают и нормальные , и касательные напряжения (см. рис. 1.2, б), равные

, . (1.10)

Формулы (1.10) показывают, что наибольшие нормальные напряжения возникают в поперечных сечениях, а наибольшие касательные ─ на площадках под углом , на которых касательные и нормальные напряжения одинаковы по величине: , .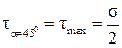

а
б

Рис. 1.2

Этот факт позволяет обьяснить реальное сопротивление растяжению и сжатию разных материалов. Рассмотрим широко распространённые конструкционные материалы: сталь и чугун. Сталь, как пластичный материал, при сжатии деформируется за счёт сдвига, и наибольший сдвиг получает от наибольших касательных напряжений под углом , при достижении этими напряжениями величины предела текучести стали при сдвиге τ_т (т. е. при 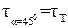) наблюдается интенсивный сдвиг по этому направлению, а образец принимает бочкообразную форму (рис. 1.3, а). Известно, что предел текучести стали при сдвиге τ_т составляет приблизительно 0,6 от предела текучести при растяжении-сжатии σ_т. Отсюда понятно, что при τ_α=τ_т образец не разрушается ни от сжимающих напряжений в поперечном сечении , которые меньше предела текучести (т. е. образец не раскалывается), ни от растягивающих напряжений в наклонных сечениях , которые больше предела текучести (т. е. образец не разрывается), а получает большую пластичную деформацию сдвига, приводящую к бочкообразной форме. При дальнейшем увеличении напряжений деформация сдвига наростает с большой скоростью, образец сплющивается, − это говорит о том, что допускать предел текучести для стальных конструкций опасно.

а ─ Стальной образец до и после сжатия	б ─ Чугунный образец до испытания и после разрушения от сжимающей силы

Рис. 1.3

При сжатии чугунного образца (рис.1.3, б) наблюдается хрупкий скол по плоскости под углом к оси. Объяснить такое разрушение можно тем, что чугун хорошо сопротивляется сжатию и слабо растяжению. Образец разрывается от действующих под углом к оси бруса растягивающих напряжений, достигших предела прочности на растяжение : . Линия разрыва перпендикулярна направлению этих напряжений и наклонена под -45⁰ к оси бруса. Для закрепления знаний о напряжениях при расчёте ступенчатого бруса можно предусмотреть вычисление напряжений под углом к оси бруса по (1.10).

Дата добавления: 2015-07-11