
Читайте также:
|
В плоской стержневой системе (рис. 1.4, а) абсолютно жёсткий брус 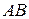 имеет три опорных стержня и несёт нагрузку известной величины.
имеет три опорных стержня и несёт нагрузку известной величины.
Требуется:
1. С помощью уравнений равновесия определить усилия в опорных стержнях.
2. Подобрать площади поперечного сечения стержней из условия прочности по допускаемым напряжениям, если допускаемое напряжение на сжатие  МПа, на растяжение
МПа, на растяжение  =40МПа. Назначить размеры сечений, принимая два стержня круглого и один квадратного сечений.
=40МПа. Назначить размеры сечений, принимая два стержня круглого и один квадратного сечений.
Исходные значения: 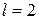 м;
м; 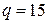 кН/м;
кН/м; 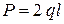 ; стержни 1, 2 - круглого сечения, стержень 3 – квадратного.
; стержни 1, 2 - круглого сечения, стержень 3 – квадратного.
Решение
1. Определение продольных усилий в опорных стержнях
Опорные стержни 1, 2, 3 имеют (рис. 1.4, б) по концам шарниры. При действии внешних сил на жёсткий брус АВ эти стержни деформируются (т.е. изменяют длину) и за счёт деформаций шарниры  и
и  перемещаются: на рис. 1, в для шарнира
перемещаются: на рис. 1, в для шарнира  показано новое положение
показано новое положение 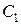 , при котором соединяемые элементы (брус АВ и стержень 2) поворачиваться друг относительно друга, и край
, при котором соединяемые элементы (брус АВ и стержень 2) поворачиваться друг относительно друга, и край  получил горизонтальное и вертикальное перемещения. Эти перемещение края
получил горизонтальное и вертикальное перемещения. Эти перемещение края  произошли от горизонтального и вертикального воздействия со стороны бруса
произошли от горизонтального и вертикального воздействия со стороны бруса 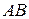 . Обозначим их как
. Обозначим их как 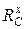 и
и 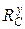 и покажем эти усилия на рис. 1.4, г. Законченный поворот стержня 2 говорит о том, что для него соблюдается условие равновесия
и покажем эти усилия на рис. 1.4, г. Законченный поворот стержня 2 говорит о том, что для него соблюдается условие равновесия 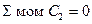 . Запишем его:
. Запишем его:
 .
.
Здесь равенство нулю возможно, если проекции  и
и  равны нулю, т. е. полная реакция
равны нулю, т. е. полная реакция 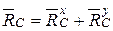 направлена вдоль стержня. Тогда в сечении
направлена вдоль стержня. Тогда в сечении 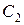 возникает реакция
возникает реакция 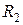 =
= 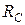 , направленная в противоположную сторону вектора
, направленная в противоположную сторону вектора 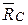 .
.
Очевидно, для стержня, имеющего по концам шарниры, будут всегда верны эти рассуждения, и, используя их, будем сразу направлять реакции вдоль такого стержня.
Замечание 1: стержень, имеющий по концам шарниры, может быть только либо растянут, либо сжат.
Для подбора размеров сечений небходимо знать, какое внутреннее усилие возникает в каждом из стержней 1, 2, 3. Внутренние усилия определяют методом сечений. Например, разрежем стержень 2 в каком-либо месте и рассмотрим одну, пусть, нижнюю часть (рис. 1.4, д). Она нагружена реакцией 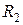 (это внешняя для стержня нагрузка) и силой
(это внешняя для стержня нагрузка) и силой 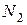 (это внутреннее для стержня усилие). Равновесие возможно, если
(это внутреннее для стержня усилие). Равновесие возможно, если  (рис. 1, д). В виду этого можно обозначать реакции опорных стержней как
(рис. 1, д). В виду этого можно обозначать реакции опорных стержней как 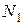 ,
, 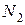 ,
,  (рис. 1.4, б) и направлять их вдоль стержней.
(рис. 1.4, б) и направлять их вдоль стержней.
Заметим, что для условия прочности важно знать направление продольной силы, которая оценивается знаком: если сила  направлена от проведённого сечения и растягивает стержень, то она считается положительной, если сжимает, то она направлена к сечению и в её цифровом значении ставится знак «–».
направлена от проведённого сечения и растягивает стержень, то она считается положительной, если сжимает, то она направлена к сечению и в её цифровом значении ставится знак «–».
Чтобы автоматически при расчёте получить правильный знак  , поставим для всех стержней направление усилий
, поставим для всех стержней направление усилий 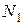 ,
, 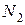 ,
,  положительное, т. е. растягивающее.
положительное, т. е. растягивающее.
| а | 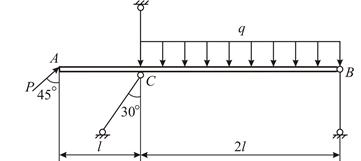
|
| б | 
|

| |
| в г д |
Рис. 1.4
Усилия 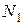 ,
, 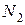 ,
,  должны удовлетворять условиям равновесия бруса
должны удовлетворять условиям равновесия бруса 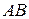 . Брус нагружен внешней нагрузкой
. Брус нагружен внешней нагрузкой 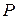 и
и 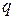 и усилиями
и усилиями 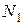 ,
, 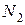 ,
,  , которые представляют в совокупности плоскую систему сил, поэтому для бруса
, которые представляют в совокупности плоскую систему сил, поэтому для бруса 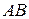 имеем три уравнения равновесия:
имеем три уравнения равновесия:
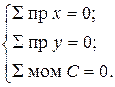
Запишем эти равнения:

Из третьего уравнения
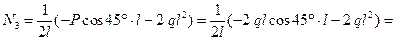
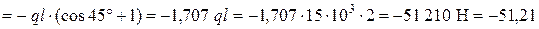 кН.
кН.
Продольное усилие 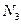 отрицательно, значит, стержень 3 сжат.
отрицательно, значит, стержень 3 сжат.
Из первого уравнения
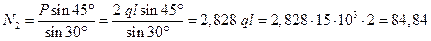 кН.
кН.
Продольное усилие 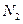 положительно, значит, стержень 2 растянут.
положительно, значит, стержень 2 растянут.
Из второго уравнения
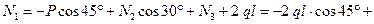
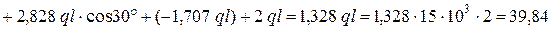 кН.
кН.
Продольное усилие 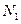 положительно, значит, стержень 1 растянут.
положительно, значит, стержень 1 растянут.
Для проверки правильности найденных усилий в опорных стержнях составим уравнение равновесия:  :
:
 ,
,
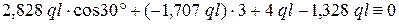 ,
,
 ,
,
значит, существует тождество 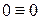 , которое говорит, что усилия в стержнях найдены верно.
, которое говорит, что усилия в стержнях найдены верно.
2. Подбор размеров поперечного сечения стержней.
Подбор размеров сечения стержней выполняется по условию прочности по допускаемым напряжениям при растяжении-сжатии (1.4), согласно которому для каждого стержня
 , (1.11)
, (1.11)
где  – нормальное напряжение;
– нормальное напряжение; 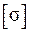 – допускаемое нормальное напряжение, причём если стержень растянут, то принимаем
– допускаемое нормальное напряжение, причём если стержень растянут, то принимаем  , если сжат, то
, если сжат, то 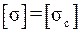 ;
;  – продольное усилие в стержне;
– продольное усилие в стержне;  – поперечное сечение стержня. Пусть стержень 1 ‒ квадратного сечения, стержни 2 и 3 ‒ круглого.
– поперечное сечение стержня. Пусть стержень 1 ‒ квадратного сечения, стержни 2 и 3 ‒ круглого.
Для 1-го стержня квадратного сечения площадь 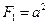 , где
, где  – сторона квадрата. Стержень 1 растянут, условие прочности (1.11) для него принимает вид
– сторона квадрата. Стержень 1 растянут, условие прочности (1.11) для него принимает вид
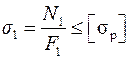 .
.
Подставляя выражение площади квадратного сечения, получим
 ,
,
откуда 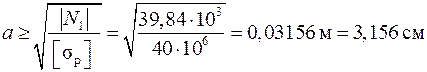 .
.
Принимаем 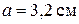 .
.
Замечание 2: полученное из условия прочности значение размеров сечения округляется в бо'льшую сторону.
Для 2-го стержня круглого сечения площадь поперечного сечения  , где
, где 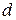 – диаметр стержня. Стержень 2 растянут, поэтому условие прочности (1.11) для него принимает вид
– диаметр стержня. Стержень 2 растянут, поэтому условие прочности (1.11) для него принимает вид
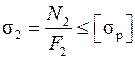 .
.
Подставляя выражение площади стержня 2 как 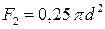 , получим
, получим
 ,
,
Откуда  .
.
Принимаем в соответствии со знаком «больше либо равно» 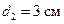 .
.
Составим условие прочности для 3-го стержня. Стержень 3 сжат, то по условию (1.11)
 .
.
Замечание 3: для сжатого стержня в условие прочности ставим модуль продольной силы.
Подставляя площадь круглого сечения  , получим
, получим
 ,
,
Откуда 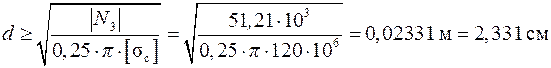 .
.
Принимаем  .
.
Дата добавления: 2015-07-11; просмотров: 744 | Нарушение авторских прав