Читайте также:
|
Стальной ступенчатый брус (рис. 1.11) жёстко защемлён с торцов и несёт нагрузку известной величины. Площади поперечного сечения и длины участков заданы.
Требуется:
1. Используя условие равновесия и уравнение перемещений, найти величины реактивных сил, возникающих в жёстких заделках.
2. Построить эпюры продольных сил N, нормальных напряжений σ, относительных деформаций e и продольных перемещенийδ.
3. Указать опасное сечение и значениеσmax, проверить прочность при допускаемом напряжении [σ]=200Мпа. Если условие прочности не удовлетворяется, указать при каких размерах площади сечений оно выполнимо.
4. Указать значения emax и δmax, проверить жёсткость при допускаемой относительной деформации [e] = 0,005 и допускаемом продольном переме- щении [δ] = 0,5мм. Если условие жёсткости не удовлетворяется, указать при каких размерах площади сечений оно выполнимо.
5. Для опасного сечения бруса вычислить касательные τα и нормальные sα напряжения в наклонной площадке, проведенной под углом α = 450 к оси бруса.
6. Вычислить температурные напряжения, возникающие в брусе при повышении температуры среды на 500 С. Принять коэффициент линейного удлиненияa = 1,25∙10-5 1/град.
7. Как изменятся величины реактивных сил, если между левой заделкой и торцом бруса будет зазор величиной 0,0001∙ L 1?
Рис. 1.11
Решение
1. Вычисление реактивной силы заделки
В этой задаче так же использована унифицированная схема ступенчатого бруса при растяжении-сжатии. Пусть в нашем примерезаданы следующие величины: сосредоточенная сила Р=- 30кН;интенсивность распределённой нагрузки по участкам: q 1=60кН/м, q 2=0; длины участков 1 1=0,5м, 1 2=0,6м; площади сечений участков F 1=5см2, F 2=3см2.
Сначала по исходным данным изобразим в масштабе заданный брус и действующую на него нагрузку (рис. 1.12, б). Брус имеет два грузовых участка (нумерацию участков начинаем справа) и две заделки, в которых возникают реактивные силы R A и RВ. Для решения задачи необходимо найти величины этих сил. Составим уравнение равновесия бруса по (1.1) 
:
.
Как видно, в уравнении имеем два неизвестных, и задача отыскания реакций является статически неопределимой. Составим дополнительное уравнение − уравнение перемещений, записав перемещение правой заделки и приравняв его нулю. Используем (1.6), запишем перемещение как сумму деформаций от каждого воздействия, начиная с левого торца бруса. Получим
.
Отсюда RA =5кН, а из уравнения равновесия найдём вторую реакцию: RВ =5кН.
2. Построение эпюр продольных сил, нормальных напряжений, относительных деформаций и продольных перемещений
Для оценки прочности и жёсткости бруса необходимо найти значения и построить эпюры продольных сил N, нормальных напряжений σ, относительных деформаций e и продольных перемещений δ. Запишем требуемые алгебраические выражения и вычислим значения, используя метод сечений и известные формулы.
1 -й участок: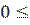 
z 1 
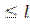1= 0,5м. В текущем сечении 1-го участка на расстоянии z 1, продольная сила N 1, напряжение σ1 и относительная деформация ε1 согласно (1.2), (1.3) и закона Гука, по которому 
, получаем
,
.
| а | 
|
| б | |
| в | |
| г | |
| д | |
| е |
Рис. 1.12
,
.
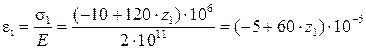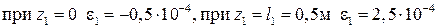2 -й участок: 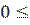z 2 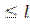2= 0,6м. В текущем сечении 2-го участка,
.
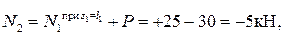
По полученным значениям продольных сил, напряжений, относительных деформаций непосредственно под брусом построим эпюры этих величин и подпишем их характерные значения (рис. 1.12, в, г, д).
Перейдём к перемещениям. Составим выражения продольных смещений δ характерных поперечных сечений А, В, С. Для этого вычислим абсолютные деформации участков по формуле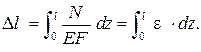 
Получаем следующие значения:
.
.
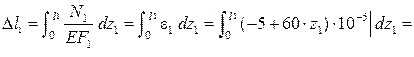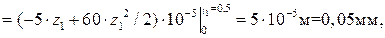
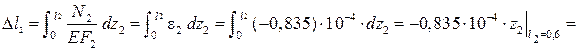
Реальное перемещение сечения заделки отсутствует,поэтому запишемперемещениеδ В = 0. Последнее сечение 1-го участка (сечение С) получило перемещение δ С, которое равно деформации этого участка:δ С =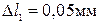 
.Последнее сечение 2-го участка (сечение А) не имеет смещения, так как в нём заделка. Действительно, получаем
На эпюресил N наклонная прямая пересекает ось (рис. 1.12, б) на расстоянии zo от начала 1-го участка (это сечение К). В этом сечении на эпюре перемещений ожидается экстремум (перегиб кривой перемещений). Используя выражение продольной силы на 1-м участке, запишем уравнение NК = 0:
, отсюда 
м.
Знаяабсциссу zо сечения К, найдём значение экстремального перемещения δ К (перемещения при z=z о) на основании (1.7) как сумму перемещенияδ В и деформации куска z о
.
Отложив полученные значения перемещений, построим под брусом эпюру δ (рис. 1.12, е).
3 и 4. Проверка условий прочности и жёсткости бруса
Далее, для ответа на пункты 3 и 4, назовём максимальные напряжения σmax, деформации ε мах, перемещения δмах и сделаем выводы о прочности и жёсткости бруса при заданных величинах допускаемых напряжений [σ]=200МПa, деформаций [ε]=0,005 и перемещений [δ] = 0,5мм:
σmax=50МПа < [σ]=200MПa, εmax = 0,00025< [ε] = 0,005, δмах=0,05мм < [δ] = 0,5мм,
и, следовательно, прочность жёсткость бруса обеспечена.
5. Вычисление напряжений в наклонной площадке
Для опасного сечения бруса вычислим касательныеτα и нормальные sα напряжения в наклонной площадке, проведённой под углом α=450 к оси бруса. Опасным сечением является сечение, в котором нормальные напряжения максимальны по абсолютной величине: в нашем примере это последнее сечение 1-го участка и σmax=50МПа. Вычислим напряжения в наклонной площадке:
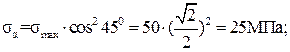
7. Вычисление температурных напряжений
Найдём температурные напряжения, возникающие в брусе при повышении температуры среды на 500С. Для этого составим уравнение перемещений, учитывая удлинение от температуры и сжатие от реакций, возникающих в заделках:
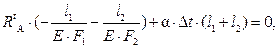
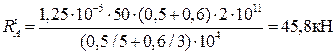
Вычислим наибольшие температурные напряжения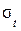 
, которые будут возникать в более тонком месте − на 2-м участке:
7. Влияние зазора на величину реакций
Оценим влияние зазора на величину реакций от нагрузки. В случае зазора при действии нагрузки торец бруса переместиться за счёт деформации на величину зазора. Поэтому величины реактивных сил должны удовлетворять уравнению перемещений, в котором правая часть равна 0,0001∙ L 1:
Получаем RA =1,7кН, RВ =1,7кН. Как видим, значение реакций при наличии зазора уменьшается.
Дата добавления: 2015-07-11; просмотров: 530 | Нарушение авторских прав