|
Читайте также: |
1. Доказать справедливость следующих логических отношений:
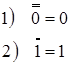
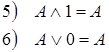
2. Доказать закон исключённого третьего:
3. Доказать закон де Моргана:
4. Доказать закон двойного отрицания: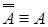 
5. Доказать закон отрицания:
- для конъюнкции;
- для дизъюнкции.
6. Доказать закон идемпотентности:
- для конъюнкции;
- для дизъюнкции.
7. Доказать коммутативный закон:
; 
8. Доказать закон поглощения:
; 
9. Доказать закон двойственности (теорема де Моргана):
; 
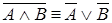10. Доказать дистрибутивный закон:
;
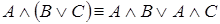11. Проверить тождество: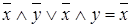 
12. Доказать ассоциативный закон:
;
13. Упростить выражение:
14. Записать на языке логических формул высказывание: точка M(x, y) находится либо на окружности с центром в начале координат, либо на биссектрисе первого координатного угла.
15. Записать на языке логических формул высказывание: точка M(x, y) является точкой пересечения трёх окружностей.
16. Записать на языке логических формул высказывание: точка M(x, y) является либо точкой пересечения двух окружностей, либо двух эллипсов.
17. Установить логическую зависимость в документе реквизитов «сумма к выдаче», «табельный номер», «фамилия», если известно, что в документе реквизит «сумма к выдаче» должен быть обязательно и должен быть один из реквизитов «табельный номер» или «фамилия». Возможно также совместное присутствие двух последних реквизитов.
18.
 |
19.
 |
20.
 |
21. Записать на языке логических формул:
 |
22.
 |
23.
|
Дата добавления: 2015-07-11; просмотров: 89 | Нарушение авторских прав