Перевод чисел из одной системы счисления в другую

Читайте также:

I Всебелорусский съезд (конгресс) в Минске в декабре 1917 г. и его решения. Провозглашение Белорусской народной республики и ее уставные грамоты
I.I. Предмет фразеологии. Виды и признаки фразеологизмов. Особенности перевода фразеологизмов.
IV. Перепишите и переведите предложения, обращая внимание на употребление модальных глаголов. Подчеркните модальные глаголы в английских предложениях и в переводе.
IV. Перепишите и переведите предложения, обращая внимание на употребление модальных глаголов. Подчеркните модальные глаголы в английских предложениях и в переводе.
IV. Перепишите и переведите предложения, обращая внимание на употребление модальных глаголов. Подчеркните модальные глаголы в английских предложениях и в переводе.
IV. Перепишите и переведите предложения, обращая внимание на употребление модальных глаголов. Подчеркните модальные глаголы в английских предложениях и в переводе.
IV. Перепишите и переведите предложения, обращая внимание на употребление модальных глаголов. Подчеркните модальные глаголы в английских предложениях и в переводе.

3.1. Перевод целых чисел

В связи с использованием в ЭВМ различных систем счисления, возникает необходимость перевода чисел из одной системы счисления в другую. Существует несколько правил перевода чисел.

Чтобы вывести правило перевода целых чисел, воспользуемся тем очевидным фактом, что, если числа А и q есть целые положительные, то всегда существует единственное (неотрицательное) целое число r, меньшее, чем q, и единственное число S, такие, что

Например, А=5, q=3, тогда

Используем это обстоятельство для перевода целого числа с основанием р, например А_р, в его эквивалент А_q с основанием q. Другими словами, мы хотим определить неотрицательные числа а₀, а₁,...,а_n, каждое из которых меньше, чем q так, чтобы

А_p=а_n·qn+...+а₁·q1+а₀·q0=А_q.

Заметим, что

|← целая часть →|← дробная часть

С другой стороны, согласно выше сформулированному утверждению, для любой пары целых положительных чисел А_р и q всегда найдется единственное S₀ и r₀ такие, что

Поскольку и частное и остаток единственны, то, приравнивая целые и дробные части, получим:

а₀=r₀; S₀=a_n·qn-1+...+а₁q0,

т.е. младшая искомая цифра равна остатку от деления А_р на q. Деля S₀ на q, и, используя предыдущий результат, получим:

откуда а₁=r₁ и т.д. до получения частного, которое меньше нового основания. Это частное и будет последней (старшей) цифрой искомого числа.

В самом деле, пусть А₁=а₃q3+а₂q2+а₁q1+а₀q0, тогда

| A2 |

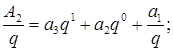
| A3 |

В связи с этим можно сформулировать следующее правило перевода целых чисел.

Целое число в новой системе счисления можно получить в результате последовательного деления исходного числа, а затем и частных, на новое основание системы до получения частного, которое меньше нового основания. Из этого частного и всех полученных остатков составится число в новой системе: последнее частное будет первой цифрой числа, последний остаток – второй цифрой, и т.д. Деление выполняется по правилам той системы счисления, в которой записано исходное число. Делитель (основание новой системы) записывается цифрами новой системы.

На практике иногда поступают так: на бумаге проводят справа от исходного числа вертикальную черту, под самим числом записывают получающиеся частные, а справа от черты друг под другом остатки. Тогда после окончания процесса полученное двоичное число переписывают снизу вверх, например, десятичное число 35 в двоичную систему переводится так:

35 1