
Читайте также:
|
Мы можем использовать для этого теорему Пифагора;
Н =sqrt (х2 + у2)
Это прекрасная формула, но ужасно сложная для ПК, поскольку вычисление квадратного корня — процесс весьма медленный и долгий. Мы, конечно, можем использовать табличное представление функции квадратного корня, но и в этом нет ничего хорошего. Есть другой, более простой способ найти удаление точки пересечения от игрока, если вычислить координаты точек и найти sin © и cos ©.
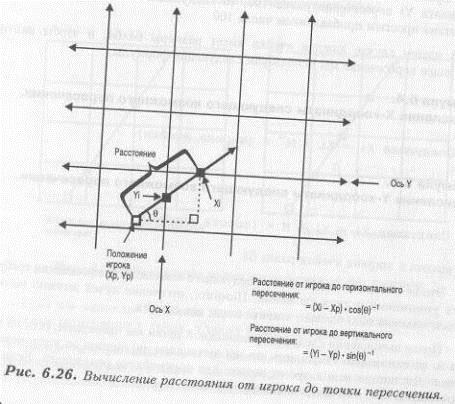
Давайте посмотрим на рисунок 6.26.
Поскольку мы уже вычислили точки вертикального и горизонтального пересечения, мы можем воспользоваться известным правилом, чтобы найти синус и косинус угла наклона:
§ Угол наклона луча (он у нас есть);
§ Длина гипотенузы (мы ее хотим найти);
§ Длина сторон треугольника (который мы имеем).
Назвав переменные так же, как они обозначены на рисунке 6.26, напишем формулы для вычисления длины- гипотенузы (или, что то же самое - искомого расстояния).
|
Дата добавления: 2015-07-12; просмотров: 266 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формула 6.3. Вычисление первой Х-координаты пересечения. | | | Вычисление масштаба |