Листинг 6.3. Описание трехмерного объекта на основе многоугольников.

// структура, описывающая объект

typedef struct object_typ

{

int num_faces; // число граней

polygon faces[max_faces]; // грани, представленные многоугольниками

float xo,yo,zo; // координаты объекта в пространстве

int visible; // виден ли объект на экране?

} object, *object_ptr;

Структура данных в Листинге 6.3 описывает объект, который образован, множеством многоугольников или поверхностей. Используя эти структуры данных и определения, мы можем создать несколько трехмерных объектов: космический корабль, планету и окружающее космическое пространство.

Чтобы поместить объекты в трехмерное пространство, мы должны знать их пространственное расположение. То есть мы должны определить значения хо, уо и zo для каждого предмета. Так же, как и в случае с двухмерными объектами (которые мы уже обсуждали в четвертой главе), пространственные объекты мы будем определять в собственных локальных системах координат (0,0,0). Затем, когда мы будем перемещать объект, мы его просто переведем в конечную позицию.

Для наших структур это будет точка (xo,yo,zo). Решением этой задачи будет простой перенос каждой из точек объекта, так же, как мы это делали для двухмерных объектов. Мы можем проверить этот метод и для объемных фигур. Например, представим себе куб, с вершиной в точке (2,2,2) (см. рис. 6.4). Если мы посмотрим на куб, то увидим, что он состоит из восьми вершин и шести поверхностей. Используя наши структуры данных, мы можем описать куб как объект с шестью гранями. Проблема, возникающая в данном случае, состоит в том, что это не самый лучший способ описания объекта. Ведь любая поверхность ограничена четырьмя точками и каждая из этих точек является общей еще для двух поверхностей. Это значит, что описание избыточно.

Возможно, более удачной окажется структура данных, содержащая список вершин. В этом случае избыточности не возникает. Однако при этом структура станет более общей и сложной, поскольку:

§ Мы должны будем иметь указатели либо индексы, или то и другое вместе для ссылки на вершины, необходимые для построения геометрической фигуры. Это увеличивает время распознавания данных объектов;

§ Наши структуры могут использовать заранее определенные массивы для хранения вершин и многоугольников. Это неэффективно использует па­мять. Массивы должны быть одного размера, так как, независимо от того, используем ли мы один элемент массива или весь массив, нам необходимо отводить место под максимальное число элементов.

Эти факты надо принимать во внимание, когда создаете структуры для трехмерных объектов. Таким образом, для наших целей структуры данных из Листингов 6.2 и 6.3 являются наиболее простыми для работы. Если же вы хотите создать набор реальных трехмерных структур, то должны использовать другую тактику.

В общем случае представление двух- и трехмерных объектов сильно зависит от игры, которую вы пишете, от размера используемой памяти и т. д. (Наша цель сейчас - понять механизмы трехмерной графики и рендеринга, а не поиск наиболее эффективных способов представления данных в компьютере. Это зависит от используемых алгоритмов и структур данных.)

Просуммируем все вышесказанное:

§ Трехмерные объекты состоят из вершин;

§ Эти вершины соединяются поверхностями или многоугольниками, которые задают границы объекта;

§ Объекты описываются относительно начала координат;

§ Существует много способов представления трехмерных объектов и вы должны выбрать тот, который устраивает вас по скорости и объему памяти.

Перемещения, масштабирование и повороты в трехмерном пространстве

Все объекты в видеоиграх представлены точками, линиями и геометрическими фигурами. Потому мы должны всегда производить их разбиение на исходные составляющие — точки. Только проделав это, мы можем их преобразовывать. Поскольку точки — это вершины объектов, то они могут рассматриваться вообще отдельно от объекта, но при этом представлять его в целом. Например, если мы хотим повернуть или переместить куб, то, прежде чем выполнять данное преобразование, нам нужно разбить объект на многоугольники, а затем на точки.

Понимая это, мы должны сосредоточить свое внимание на способах преобразования точек.

Перемещение трехмерного объекта

Для перемещения точки (x.y.z) на расстояние (dx,dy,dz) необходимо выполнить следующие операции:

x=x+dx;

y=y+dy;

z=z+dz;

Если мы хотим использовать эту матрицу, то должны представить точку в виде четырех компонентов (x,y,z, 1). Матричное умножение будет выглядеть так:

где dx, dy и dz - это перемещения по осям координат, а х', у' и z' - координаты точки после перемещения.

Масштабирование трехмерного объекта

Следующая операция трансформации, которую должны уметь выполнять, это масштабирование. Изменение размеров трехмерного объекта похоже на двухмерное масштабирование. Здесь показано масштабирование точки (x,y,z) с коэффициентом S:

х=х * S;

у=у * S;

z=z * S;

Все очень просто. Только кажется, что трехмерная графика сложна для понимания. Для описания преобразований с помощью матриц, мы опять должны представить точку в виде (x,y,z,1):

Если вы решите масштабировать каждый из компонентов по-разному, то вам потребуются разные коэффициенты для каждого измерения:

Это приведет к неоднородному масштабированию.

Вращение трехмерного объекта

Последняя трансформация, о которой мы поговорим - это вращение. Вращение трехмерного объекта аналогично двухмерной ротации; необходимо только добавить третье измерение.

Вращение, параллельное оси Х

Следующая матрица преобразований вращает точку (x,y,z) параллельно оси X:

Вращение, параллельное оси Y

Матрица преобразования, вращающая точку параллельно оси Y:

Вращение, параллельное оси Z

Матрица преобразования, вращающая точку параллельно оси Z;

Последнее слово о трехмерных трансформациях

Подведем итог разговору о трансформациях трехмерных объектов. Реализовать эти трансформации не сложно. Это только часть возможных преобразований. Существует много вариаций и несколько совершенно новых типов — деформация и т. д. В общем, мы уже достаточно знаем, чтобы перейти к проекциям.

Проекции

Сейчас мы знаем, как изобразить трехмерный объект и как произвести операции перемещения, масштабирования и поворота этого объекта. Возникает вопрос: «А как мы можем рисовать трехмерные объекты на плоском экране?» ответ прост: мы «проецируем» их на поверхность экрана.

Проекция трехмерных объектов на плоскость довольно проста и дает хорошие результаты. К сожалению, образы при этом не всегда выглядят реалистично. Ваши глаза имеют одну точку зрения, а, следовательно, образ будет похож на трехмерный, но не станет «по-настоящему» объемным.

Замечание

Существуют специальные шлемы с дисплеями, дающие стереоскопический эффект. Эта шлемы используются в системах виртуальной реальности. Проблема, возникающая с их использованием, заключается в том, что параллакс или фокальная точка различна для каждого человека. Если шлем не отрегулирован и точка не подобрана, то зритель вскоре получит сильнейшую головную боль.

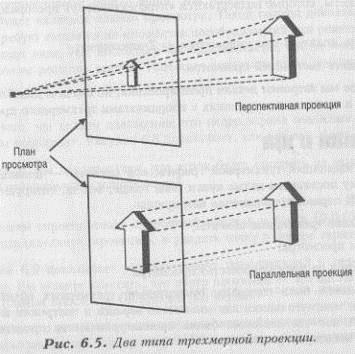
Тем не менее, мы будем использовать монитор для проецирования трехмерного образа на экран. Я хотел бы обсудить типы проекции, которые могут применяться с этой целью: параллельная, или ортогональная проекция и перспективная проекция. Рисунок 6.5 показывает диаграммы каждого типа проекций.

Параллельная проекция проста в реализации, но образы не выглядят объемными. Они, скорее, похожи на обычные плоские картинки. Для реализа ции такой проекции достаточно убрать Z-компонент каждой точки трехмерного объекта и затем нарисовать объект, как двухмерный.

С другой стороны, перспективная проекция дает большее приближение и выглядит почти «трехмерно». Она имеет качество «длинной дороги». На рисунке 6.6 изображена такая «дорога». Перспективная проекция принимает во внимание 2-компонент и соответст­венно изменяет компоненты Х и Y.

Элементы, которые подвергаются «перспективному» преобразованию, должны:

§ Просто делиться или умножаться на Z-компонент;

§ Обладать дистанцией просмотра.

Вскоре мы затронем детали проецирования, но сначала давайте поговорим об экране и его взаимоотношениях с координатами трехмерного пространства.

Копирование на экран

Создание настоящей трехмерной графической системы — довольно сложное дело. Этому посвящены целые книги (еще толще, чем та, которую вы держите в руках). В первом приближении нам нужны:

§ Кое-какие трехмерные объекты;

§ Объем просмотра;

§ Проекция на план (плоскость) просмотра.

Мы можем быть спокойны относительно трехмерных объектов — мы определили многоугольники как множество вершин и построили на их основе объекты. А вот что касается объема просмотра и плана просмотра, то тут требуются некоторые разъяснения.

Когда мы смотрим на трехмерный мир, то сами должны в нем где-то находиться и иметь направление просмотра. Рисунок 6.7 иллюстрирует эту мысль.

Учитывая, что в реальном мире мы смотрим на объекты с определенной точки и в определенном направлении, мы можем их построить на экране, который и будет являться планом просмотра. Такой подход довольно сложен, поскольку требует выполнения множества преобразований для решения данной задачи в общем виде. Но, поскольку мы программисты, нас не очень должно волновать общее решение задачи. Нам надо создавать игры, выглядящие как трехмерные.

§ Во-первых, мы делаем допущение, что центр экрана совпадает с центром системы координат. Рисунок 6.8 показывает, как она выглядит на экране;

§ Во-вторых, мы предполагаем, что игрок будет смотреть на экран вниз по оси Z (отрицательное направление).

Мы можем спроецировать одиночный пиксель в точку (0,0,0) на экран, используя параллельную проекцию, и увидеть точку в центре экрана. Рисунок 6.9 показывает разницу между параллельной и перспективной проекциями. Вы можете заметить, что центр проекции - это дистанция между игроком и планом просмотра (поверхностью экрана).

Математика для проецирования трехмерных объектов на экран сказочно проста и мы ее реализуем за пару минут. Но пока поговорим о масштабировании.

Масштабирование экрана

Поскольку в режиме 13h экран имеет размеры 320х200 точек, то возникает вопрос: «Как мы сможем увидеть вселенную размером 1000х1000 точек?» Есть много способов решения этой проблемы. Один из путей - это использование перспективной проекции. Когда мы удаляемся от объекта, он становится меньше. В некоторой точке вселенная размером 1000х1000 уменьшается настолько, что «влезает» в экран.

Если вы используете параллельную проекцию, вам не удастся добиться такого результата. Чтобы сделать это, вы должны масштабировать экран и использовать его с другими размерами. Например, для получения экрана размером 1000х1000 мы должны сделать следующее.

Чтобы нарисовать точку (х,у) на экране, где каждый из компонентов имеет диапазон измерения от 0 до 1000, мы производим преобразования

x_screen = 320 * х / 1000;

y_screen = 200 * у /1000;

где х_screen и y_screen будут истинными координатами пикселя на экране размером 320х200.

Конечно, изменив таким образом масштаб экрана, вы не получите разрешения 1000х1000 точек. Разрешающая способность останется прежней - 320х200. Более того, некоторые точки будут изображены в одних и тех же местах. Например, точки с координатами 999 и 1000 сольются в одну, и вы не сможете их различить. Но это и не столь важно, поскольку трехмерное изображение на основе многоугольников отличается от битовых изображений двухмерного мира.

Математические основы параллельных проекций

Математика, необходимая для произведения параллельной проекции, элемен­тарна - вы просто убираете z-координату и рисуете каждую точку объекта по координатам (х,у). Вот и вся трансформация. Для примера возьмем точку (x,y,z).

x_parallel = х

y_parallel= у

plot х,у

Математические основы верспективной проекции

Произведение перспективной трансформации не многим отличается от параллельной проекции. Мы используем z-компонент для масштабирования координат х и у с целью «отдаления» точки от плана просмотра (поверхности экрана), и для придания объекту более реалистичного вида.

Рассмотрим эту операцию на примере: дана точка (x,y,z), удаленная от плана просмотра на расстояние D:

x_perspective = D * х / z

y_perspective = D * у / z

Вот и все. Достаточно умножить каждый компонент на расстояние и разделить на значение Z-координаты. Образ получается похожим на трехмерный.

Объем просмотра

Мы говорили об объектах и проекциях в трехмерном пространстве, но не упоминали об объеме просмотра. Это понятие подобно области отсечения для двухмерного мира (мы это обсуждали в четвертой главе, «Механизмы трехмерной графики»). Так же, как мы отсекаем объекты у границ экрана в двухмерных играх, мы должны проделывать это и с трехмерными объектами. Видимая часть пространства имеет шесть поверхностей и чем-то напоминает трехмерную трапецию или усеченную пирамиду (см. рис. 6.10). Эта область иногда называется еще телесным углом просмотра.

В общем случае, нам нужно отсечь каждый объект или его часть, выходящую за границы телесного угла просмотра. Поскольку отсекаемые фрагменты при перспективной проекции становятся не видны, то и нет необходимости выполнять их рендеринг.

Наиболее важны ближняя и дальняя плоскости отсечения (рис, 6.10). Когда объект подходит слишком близко к экрану, то он должен исчезать (он как-бы оказывается у вас за спиной), а когда он удаляется на слишком большое расстояние, то мы его тоже можем убрать, поскольку он просто превратится при рендеринге в точку.

Я больше ничего не буду говорить про трехмерное отсечение - оно не потребуется для игр типа DOOM и Wolfenstem, но может пригодиться для создания различных «леталок» и «ездилок». Вы можете использовать ту же тактику, что и для двухмерного отсечения. Теперь нам надо познакомиться еще с одной вещью — моделированием цельных геометрических объектов.

Геометрическое моделирование

Геометрическое моделирование необходимо для придания играм большего реализма. Объекты, построенные компьютером при геометрическом моделировании, выглядит цельным. Посмотрите на рисунок 6.11, чтобы увидеть разницу между цельной геометрической и каркасной моделями.

Как видите, геометрическая модель выглядит более убедительно. Сегодня использование каркасных объектов уже нельзя назвать удовлетворительным решением. Теоретически создание цельных моделей ненамного сложнее, нежели каркасных. Мы можем использовать те же самые структуры данных, преобразования и проекции. Но когда мы пытаемся нарисовать цельный трехмерный объект, возникают определенные проблемы. Как вы понимаете, существуют еще и скрытые поверхности — те, которые не видны игроку (например, тыльная сторона рассматриваемого объекта) и которые не должны появляться на экране. Компьютер не понимает разницы между видимыми и невидимыми поверхностями. Он нарисует их, все. Чтобы избежать этого, мы должны найти способы удаления скрытых поверхностей. Сейчас мы об этом и поговорим.

Удаление невидимых поверхностей

Среди программистов, работающих в области компьютерной графики, техника удаления невидимых поверхностей считается «высшим пилотажем». Известно, что удаление невидимых поверхностей является сложной математической задачей. Существует довольно много алгоритмов для ее решения, но все они очень сложны в реализации и редко работают с приемлемой для видеоигр скоростью.

Удаление невидимых поверхностей можно разделить на две фазы:

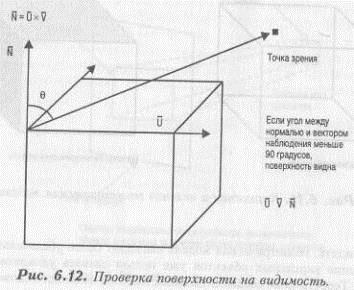
Фаза 1. Прежде всего удаляются поверхности, которые никогда не будут видны с точки зрения наблюдателя. Для этого мы должны использовать точку пересечения между вектором наблюдения и вектором нормали к каждой из рассматриваемых плоскостей. Мы вычисляем это значение. Если значение угла меньше 90°, то поверхность видна, если больше 90° - нет и она удаляется.

Фаза 2. После того как скрытые поверхности удалены, видимые плоскости должны быть окрашены. Вы должны быть уверены, что в течение этой фазы, объекты будут выглядеть правильно.

Существует популярный Алгоритм Художника, который это хорошо умеет делать. Он работает, выполняя пять тестов для каждой видимой пары многоугольников (поверхностей) и затем создает последовательность их окраски от дальней части изображения к ближней.

Другая техника создания этой последовательности носит название Алгоритма Z-буфера. Он работает в пространстве образа на уровне пикселей. Он прост в реализации, но медленно работает и требует много памяти.

Настоящие разработчики видеоигр никогда не используют эти алгоритмы в чистом виде. Мы должны создать свою систему», которая будет сочетать оба метода. Для этого детально рассмотрим каждый из них.

Алгоритм художника

Алгоритм Художника — это один из тех алгоритмов, которые могут создавать ощущение реальности. Основная идея Алгоритма Художника состоит в сортировке поверхностей таким образом, что при рендеринге это выглядит корректно. Наиболее просто этот алгоритм может быть реализован, когда каждая поверхность параллельна плану просмотра (то есть перпендикулярна лучу зрения). В этом случае нам достаточно отсортировать поверхности в порядке уменьшения значения координаты Z. Затем мы сначала нарисуем самую дальнюю поверхность, потом более близкую и т, д. Это достаточно специфичное условие, но и у него есть свои реализации.

Проблемы начинают возникать, когда поверхность не параллельна плану просмотра. При этом все/разбивается на куски и мы вязнем в выполняемых тестах. Это значит, что нам надо выполнить множество вычислений. Рисунок 6.13 показывает вид сверху вниз двух многоугольников в одном из самых неудачных случаев.

Безразлично, как мы будем сортировать эти многоугольники - по минимуму, максимуму или среднему значению Z - мы всегда получим неверный результат. Чтобы этого избежать, мы должны проделать пять тестов для каждой пары многоугольников.

Тесты выполняются только в том случае, если значения Z для двух многоугольников совпадают. Иначе, они могут рисоваться в любой последовательности.

Дата добавления: 2015-07-12