Часть 3. Расчет гидравлического прыжка. Построение кривой свободной поверхности по трассе канала

В зависимости от соотношения критических и нормальных глубин соседних участков сопряжение кривых свободной поверхности может быть плавным либо сопровождаться гидравлическим прыжком. Ранее было установлено, что в примере (см. рис. 1.7) сопряжение соседних кривых спада возможно только через гидравлический прыжок. Определим теперь место его возникновения, т. е. установим, на каком участке он возникает и где конкретно находится центр или ось гидравлического прыжка.

Из теории [1, 2] известно, что прыжок будет находиться ниже по течению, т. е. на втором участке, если глубина h", сопряженная с глубиной в конце первого участка h', будет больше бытовой, в данном случае нормальной глубины h ₀₂ второго участка. Если же h" < h ₀₂, то прыжок будет надвинут на первый участок, т. е. влево от перелома профиля дна.

Для определения места прыжка широко используется графоаналитический метод. Предварительно вычисляется и строится график прыжковой функции П(h) (рис. 3.1) по формуле:

,

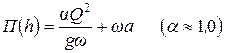где 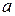— глубина погружения центра тяжести живого сечения; для трапецеидальной формы русла равна:

.

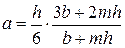Для построения графика задаются 8÷9 значениями h больше и меньше h _кр. и вычисляются величины 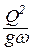, ωa и П(h). Вычисления представляются в табличной форме (табл. 3.1).

Таблица 3.1

Расчет точек прыжковой функции

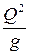
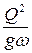
№ п/п	h, м	ω, м^2			a, м	aω, м^3	П(h)
	h кр

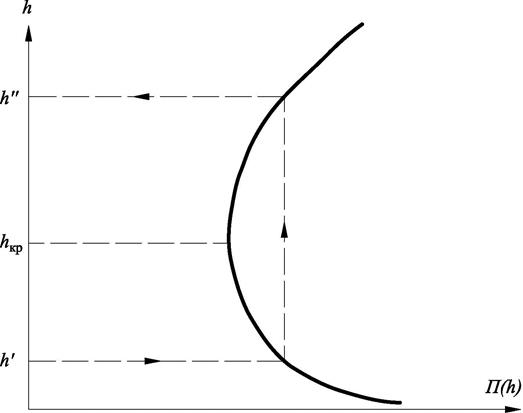
Рис. 3.1. График прыжковой функции П=f(h)

Глубина в конце первого участка равна нормальной, т. е. h ₀₁
(или h ₀₁+1 см). Это значение принимается за первую сопряженную глубину h', т. е. h ₀₁ = h', с помощью которой по графику прыжковой функции определяется h" и сравнивается с h ₀₂.

Рассмотрим два возможных варианта:

· прыжок на втором участке (h" > h ₀₂);

· прыжок на первом участке (h" < h ₀₂).

В первом случае для нахождения оси прыжка рассчитывается и строится на втором участке кривая подпора типа С ₁, начиная от точки перелома профиля дна, т. е. от глубины h ₁ =h'(h ₀₁ ) до h ₂ =h _кр. Расчет кривой, являющейся продолжением кривой свободной поверхности первого участка, выполняется на ПК. Далее по графику прыжковой функции определяются глубины h", сопряженные выбранным 5÷6 значениям глубин кривой подпора С ₁. Точка пересечения пунктирной кривой сопряженных глубин h" с основной кривой спада В ₁ на этом участке определяет местоположение оси прыжка (рис. 3.2).

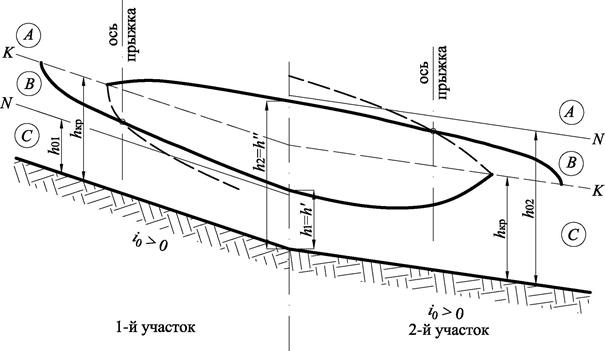
Рис. 3.2. К определению местоположения прыжка

Если прыжок расположен на первом участке, то расчет (ручным способом или на ПК) кривой подпора типа А ₂ ведется от глубины h ₁ =h"(h ₀₂ ) до h ₂ =h _кр. Эта кривая является продолжением кривой свободной поверхности второго участка в сторону первого участка. Аналогично предыдущему для 5÷6 значений глубин h" кривой А ₂ по графику прыжковой функции находятся соответствующие им значения глубин h'. Полученная в результате точка пересечения пунктирной кривой изменения глубин h' с кривой спада В ₂, первого участка определяет положение оси прыжка (см. рис. 3.2).

Потери энергии в прыжке Δ Э определяются как разность удельной энергии сечения до прыжка Э(h ₁ ) и после прыжка Э(h ₂ ). Задаваясь рядом значений глубин h больше и меньше h _кр, вычисляется удельная энергия сечения (табл. 3.2)

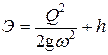
и строится график Э(h) (рис. 3.3). По графику, зная сопряженные глубины на оси прыжка, определяются соответствующие им значения удельной энергии Э( 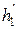) и Э( 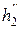). Следовательно, потери энергии в прыжке равны:

.

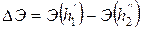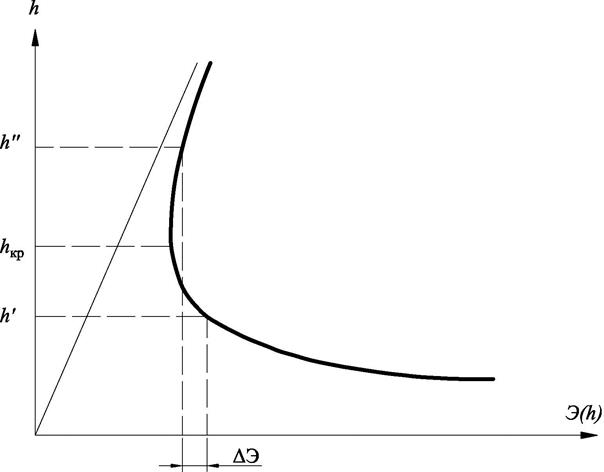
Рис. 3.3. График энергии потока Э(h)

Таблица 3.2

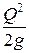
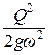
№ п/п	h, м	ω, м^2	ω ^2			Э(h), м
	…
	h кр
	…

Для получения более точных результатов при построении графиков прыжковой функции и удельной энергии следует выбирать масштаб шкалы h в несколько раз большим, чем для П(h) и Э(h). В заключение третьей части работы строится в масштабе общий график кривой свободной поверхности вдоль всей трассы канала. При этом следует применять искаженный масштаб, т. е. вертикальный масштаб глубин и уклонов брать крупнее продольного масштаба длин.

ЛИТЕРАТУРА

1. Мелконян Г.И. Основы гидравлических расчетов на водных путях. Учеб. пособие. Л.: ЛИВТ, 1978.

2. Чугаев P.Р. Гидравлика. — М. Л.: ГЭИ, 1971.

3. Павловский Н.Н. Краткий гидравлический справочник. — М.: Стройиздат, 1940.

4. Киселев П.Г. Справочник по гидравлическим расчетам. — М.: ГЭИ, 1957.

5. Мостков М.А. Гидравлический справочник. — М.: ГЭИ, 1964.

6. Справочник по гидравлике. / Под ред. И.А. Колышкова. — Киев, Высш. школа, 1977.

Дата добавления: 2015-07-10