Часть II. Численный расчет кривых свободной поверхности по участкам канала

Численный расчет кривых свободной поверхности проводится по уравнениям, полученным Б. А. Бахметьевым после преобразования и последующего приближенного интегрирования дифференциального уравнения движения (1.4).

Для русла I- го типа (i ₀ > 0) решение записывается в виде:

.

(2.1)

Здесь , η ₂ = — относительные глубины;

h ₁ и h ₂ — действительные глубины в рассматриваемых сечениях потока;

l — расстояние между этими сечениями;

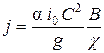— вспомогательная величина, характеризующая отношение кинетической энергии потока к его потенциальной энергии;

α — коэффициент кинетической энергии, принимаемый равным 1,10;

— функция, численные значения которой берутся из гидравлических справочников [3÷6] в зависимости от η и x, где х — гидравлический показатель русла (методика определения приводится ниже).

Для русла II- го типа (i ₀ < 0):

.

Здесь и 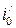— соответственно «фиктивные» нормальная глубина и уклон;

— относительная глубина;

— вспомогательная величина;

— функция, численные значения которой берутся из гидравлических справочников в зависимости от ξ и x, где х — гидравлический показатель русла.

Для русла III- го типа (i ₀ = 0):

;

здесь , — относительные глубины;

— вспомогательная величина;

— функция, численные значения которой берутся из гидравлических справочников в зависимости от ξ и x.

Гидравлический показатель русла x определяется для каждого участка канала по гидравлическим справочникам в зависимости от заданного коэффициента заложения откоса и отношения средней глубины на данном участке к ширине канала по дну, т. е. h _ср /b. Средняя глубина определяется как полусумма начальной и конечной глубин на данном участке. Так в приведенном выше примере для кривой спада (см. рис. 1.7) начальная глубина на первом участке h _нач =h _кр, а конечная — h ₀₁, следовательно, .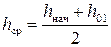

Гидравлический показатель русла может быть также найден и из показательной зависимости Б. А. Бахметьева:

,

откуда

,

где K _ср и h _cp — соответственно средние значения модуля расхода и глубины на участке канала. Вычисленное значение гидравлического показателя округляется до 0,25.

Ручной способ расчета кривых свободной поверхности вне зависимости от типа русла заключается в разбивке разницы глубин на концах участка на 5÷6 (желательно одинаковых) интервалов и последующем расчете расстояний Δ l между этими глубинами. Сумма расстояний Δ l определяет длину участка с неравномерным движением.

Выполним расчет кривой спада на первом участке рассматриваемого выше примера (см. рис. 1.7). Так как здесь русло I-го типа, то используется уравнение (2.1). Расчет следует представлять в табличной форме.

Расчет средних значений вспомогательной величины j _cp (5÷6 значений) необходимо вести в форме табл. 2.1.

Таблица 2.1

№ п/п	h 1, м	h 2, м	h ср, м	B, м	ω, м^2	х	R, м	С	С ^2	j cp

Далее необходимо выполнить расчет расстояний Δ l между выбранными значениями глубин h ₁ и h ₂ (табл. 2.2).

Таблица 2.2

№ п/п	h 1, м	h 2, м	j cp	η 1	η 2			Δ l, м

Если интервалы между глубинами выбраны одинаковыми, то значения Δ l будут увеличиваться в случае кривых спада и уменьшаться для кривых подпора, что позволяет контролировать правильность выполняемого расчета.

При расчете кривой спада (см. рис. 1.7) за начальное значение h ₁ принимается заданная глубина h _нач = h _кр, а за конечное h ₂ ― h ₀₁ + 1см. (Если принять h ₂ =h ₀₁, то получим из уравнения (2.1) l = ∞, так как кривая спада носит асимптотический характер). Для получения положительных значений Δ l нумерацию глубин следует брать по течению. Однако, иногда (например, при расчете кривой спада на втором участке) начальная глубина может быть задана в конце участка. В этом случае расчет удобнее вести против течения, а значения Δ l будут получаться отрицательными.

Полученное значение ΣΔ l может оказаться как больше, так и меньше заданной длины участка канала l.

Тогда в первом случае следует изменить глубину (в сторону увеличения) в конце участка h ₂с таким расчетом, чтобы ΣΔ l оказалась равной заданной длине участка l, т. е. необходимо найти методом подбора фактическую глубину в конце участка h ₂, которая будет больше принятой ранее h ₀₁ + 1см.

Во втором случае, когда полученная длина участка с неравномерным течением ΣΔ l оказывается меньше заданной длины участка l, то это означает, что далее до конца заданного участка устанавливается равномерный режим течения с глубиной, равной нормальной глубине потока, и кривая спада будет асимптотически стремиться к нормальной глубине.

Для расчета кривой свободной поверхности на втором участке и при расчетах русел другого типа составляются аналогичные таблицы.

Заметим, что на правильность расчетов большое влияние оказывает тщательность определения из таблиц гидравлического справочника значений функций Бахметьева Б(η) по относительным глубинам η или ξ. При отсутствии в таблице промежуточных значений необходимо делать линейную интерполяцию.

Расчеты кривых свободной поверхности остальных участков выполняются на ПК (см. приложение). Результаты расчетов прилагаются к записке по II- й части работы.

Дата добавления: 2015-07-10