|
Читайте также: |
Задача по определению нормальной глубины h 0 из уравнения Шези решается обычно графоаналитическим методом путем построения графика K=f(h). Уравнение Шези записывается в виде:
 ,
|
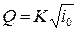где K=ω·С· 
— модуль расхода;
i 0 — уклон дна;
ω — площадь сечения потока;
— коэффициент Шези;
R=ω/χ — гидравлический радиус;
п — коэффициент шероховатости;
χ — смоченный периметр.
Предварительно определяется модуль расхода, соответствующий заданному расходу и уклону дна данного участка канала:
 .
|
Затем, задаваясь произвольными 5÷6 значениями глубины h, последовательно вычисляются ω, χ, R, С и, наконец, K. Полученные значения K обязательно должны быть как больше, так и меньше ранее найденного значения K зад. Если значения K оказываются существенно отличными от K зад, следует изменить выбранные ранее значения глубин h таким образом, чтобы соответствующие им K не отличались от K задболее, чем на ±(30…50)%.Вычисления удобно выполнять в табличной форме (табл. 1.1).
Таблица 1.1
Участок №… (K зад=…)
| № п/п | h, м | χ, м | ω, м2 | R, м |
| С | K |
Значения ω, χ и ширины канала по зеркалу В для трапециевидных русел определяются по формулам (рис. 1.1):
 ,
| (1.1) |
 ,
| (1.2) |
 ,
| (1.3) |
где b — ширина канала по основанию;
m — заданный коэффициент заложения откоса.
Рис. 1.1. Поперечное сечение трапециевидного канала
Для прямоугольных русел величина заложения откоса равна нулю, поэтому зависимости (1.1÷1.3) преобразуются в следующий вид:
,
,
.
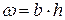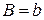По данным таблицы строится график (рис. 1.2), на котором показана последовательность определения h 0 для данного участка. Аналогичные вычисления и построения выполняются и для других участков канала, уклоны дна которых не равны нулю (при уклоне дна, равном нулю, h 0 =∞).
На участках с отрицательным уклоном дна для последующих расчетов необходимо по той же методике найти так называемую «фиктивную» нормальную глубину потока 
, т. е. глубину потока, который двигался бы по данному участку канала с тем же расходом, но в обратную сторону по уклону дна:
Рис. 1.2. Определение нормальной глубины h 0
Таким образом, для участков с отрицательным уклоном:
 .
|
Для нахождения критической глубины h кр также используется графоаналитический способ. В этом случае строится график 
(рис. 1.3). Учитывая, что при h = h кр соблюдается равенство
 ,
|
то по заданному расходу можно найти h кр. Вычисления выполняются в табличной форме (табл. 1.2).
Таблица 1.2
| № п/п | h, м | ω, м2 | ω3 | B, м | 
| Примечание |
| ||||||
Рис. 1.3. Определение критической глубины в канале
Аналогично предыдущему при вычислениях берется 5÷6 произвольных значений глубин h, при которых полученные величины будут в пределах ±(30…50) % от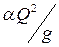 
, а точки на графике должны находиться по обе стороны от значения .
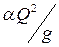Для русел прямоугольного сечения существует аналитическая зависимость для вычисления критической глубины:
 ,
|
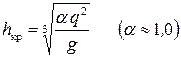где q=Q/B — удельный расход.
Критический уклон i кр, при котором для данной формы русла и заданного расхода h 0= h кр, определяется по формуле:
 ,
|
где 
, 
, 
— соответственно, значения смоченного периметра, коэффициента Шези и ширины по зеркалу при глубине в канале h кр.
Критический уклон можно также определить и графоаналитическим способом [1], используя имеющиеся графики K=f(h) и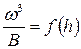 
.
Для определения вида кривых свободной поверхности используется уравнение неравномерного движения
 ,
| (1.4) |
где 
— гидравлический уклон,
или его модификация
 .
|
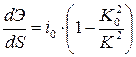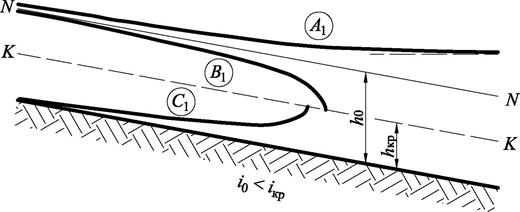
В результате качественного анализа этих уравнений [1] удается для всех типов русел устанавливать виды кривых свободной поверхности, встречающиеся в практических расчетах. Вид кривой на данном участке определяется типом русла, соотношением глубин h 0и h кp и зоной течения («А», «В» или «С»). Для русла I- го типа (i 0 > 0) кривые свободной поверхности показаны на рис. 1.4. Все кривые обозначены буквой соответствующей зоны с цифровым индексом (1, 2, 3), обозначающим возможное соотношение глубин h 0 и h кр:
1 — h 0 > h кр (i 0 < i кp);
2 — h 0 < h кр (i 0 > i кр);
3 — h 0 = h кр (i 0 = i кр).
| а) |
|
| б) |
|
| в) |
|
Рис. 1.4. Виды кривых свободной поверхности при i 0 > 0
Для русел II- го (i 0 < 0) и III- го (i 0 = 0) типов из-за отсутствия понятия нормальной глубины существует всего 2 зоны — «В» и «С». Кривые свободной поверхности для этих русел показаны на рис. 1.5 и 1.6, где индексы у буквенных обозначений относятся соответственно к руслам II и III типов.
Рис. 1.5. Виды кривых свободной поверхности при i 0 < 0
Рис. 1.6. Виды кривых свободной поверхности при i 0 = 0
В задании на проектирование указываются количество участков проектируемого канала, их длина, уклоны дна и глубины в начале или конце некоторых участков. Сопоставляя заданные глубины с найденными критической и нормальной глубинами, можно сделать вывод о зоне течения и виде кривой свободной поверхности на каждом участке.
Например, задан канал, состоящий из двух участков I- го типа (i 0 > 0). На первом участке нормальная глубина h 01 (индекс 1 обозначает первый участок) оказалась по расчету меньше критической, т. е. h 01 < h кр. Проверка соотношения уклонов должна при этом соответствовать неравенству i 01 > i кp. Если заданная начальная глубина на участке h нач ≤ h кр, то, понимая, что поток всегда стремится к равномерному движению, можно сделать вывод об изменении глубин h на данном участке от h нач до h 01, что соответствует зоне «В», где имеет место кривая спада типа В 2 (см. рис. 1.4).
На втором участке, расположенном ниже первого, нормальная глубина h 02 оказалась по расчету больше h кр. В этом случае уклон дна второго участка должен быть меньше критического уклона, т. е. i 02 < i кр. Пусть начальная глубина h нач на этом участке задана в конце данного участка. Предположим, что h кр ≤ h нач ≤ h 02. Следовательно, глубины потока на этом участке меняются в промежутке от нормальной глубины h 02 до h кр, что соответствует зоне «В», т. е. кривой спада типа В 1 (см. рис. 1.4).
На рис. 1.7 показан вид кривых свободной поверхности рассмотренных участков канала. Подобным образом анализируются кривые свободной поверхности для любых вариантов заданных глубин и типов русел. Их качественное (без соблюдения масштаба) изображение должно быть включено в курсовую работу.
Рис. 1.7. Пример определения вида кривых свободной поверхности
Рассматривая глубины в конце первого и начале второго участков, можно сделать вывод о том, что сопряжение кривых свободной поверхности будет осуществляться путем гидравлического прыжка, если глубина на первом участке меньше, а на втором больше критической (если обе глубины окажутся больше или меньше критической, то прыжок образоваться не может).
Таким анализом заканчивается первая часть работы.
Дата добавления: 2015-07-10; просмотров: 303 | Нарушение авторских прав