Теорема о кинетическом моменте

Теорема о кинетическом моменте имеет важное значение в теории гироскопов. С ее помощью доказываются основные свойства гироскопа, которые были рассмотрены ранее лишь стороны их внешнего проявления.

Докажем теорему о кинетическом моменте, имея в виду произ­вольное твердое тело, у которого точка неподвижна (рис. 1.3). Выделим в теле материальную точку 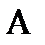, имеющую массу 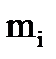. Положение точки 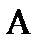вполне определяется радиусом-вектором . Предположим, что на тело в указанной точке 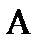действует внешняя сила . Момент этой силы относительно неподвижной точки определяется следующим векторным произведением:

Значение момента силы

Рис. 1.3. К доказательству теоремы о кинетическом моменте

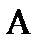Под действием силы тело приходит во вращение и каждая матери­альная точка тела, в том числе , приобретает линейную скорость . Как известно, произведение массы материальной точки на ее линей­ную скорость называется количествам движения материальной точ­ки 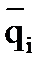. Тогда

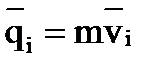
Вектор 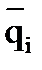имеет тоже направление, что и вектор линейной скоро­сти . Точно так же, как выше был определен момент силы относи­тельно точки , можно определить момент любого другого вектора, в том числе 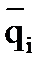. Этот момент называется моментом количества движения материальной точки массой 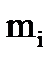относительно точки :

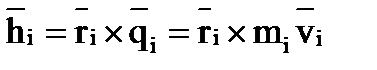
Найдем первую производную по времени от вектора момента количе­ства движения :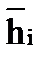

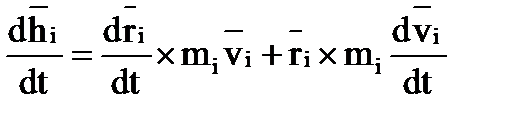(1.1)

Поскольку первая производная от радиуса-вектора по времени есть вектор скорости его конца, т. е. 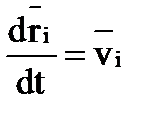, векторное произведение 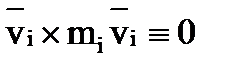как произведение коллинеарных векторов.

Следовательно, выражение (1.1) примет более простой вид:

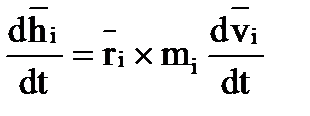(1.2)

В соответствии с формулировкой второго закона Ньютона

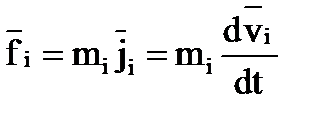(1.3)

Подставив в формулу (1.2) значение формулы (1.3), получим . Поскольку правая часть этого равенства есть момент силы относительно точки О, то .

Рассматривая твердое тело как совокупность 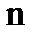материальных точек и считая, что на тело действует 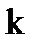внешних сил, суммируя, можем записать

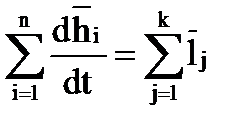(1.4)

Выражение , обозначим . Новый вектор 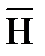- это момент количества движения тела относительно точки О или, применяя более часто употребляющийся термин, кинетический момент.

Выражение , обозначим . Вектор - это главный момент внешних сил, действующих на тело относительно точки О.

С учетом сказанного выражение (1.4) примет следующий вид:

(1.5)

Полученная формула (1.5) выражает основную теорему динамики твердого тела (теорему о кинетическом моменте): первая производная по времени от вектора кинетического момента тела равна вектору главного момента всех внешних сил, действующих на тело.

Производную от кинетического момента нужно понимать в векторном смысле.

Тогда производная 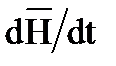есть скорость конца вектора , т.е.

(1.6)

Сопоставляя выражения (1.5) и (1.6), получим

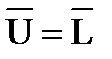(1.7)

Отсюда теорема о кинетическом моменте может быть сформулирована следующим образом: вектор линейной скорости конца вектора кинетического момента твердого тела относительно некоторой точки равен вектору главного момента всех сил, действующих на тело относительно той же точки. Эта формулировка известна под названием теоремы Резаля [1].

Рис. 1.4. К пояснению сути кинетического момента

Рассмотрим подробнее, что представляет собой кинетический момент Н применительно к гироскопу.

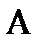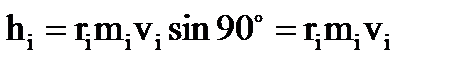Выделим в гироскопе, ротор которою имеет угловую скорость собственного вращения, точку (рис. 1.4). Момент количества движения точки относительно точки О центра подвеса гироскопа . В данном случае . Исходя из соотношения , получим . При суммировании по всем точкам ротора гироскопа найдем

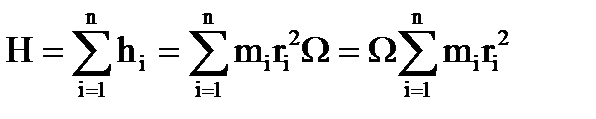
Однако есть не что иное как момент инерции ротора гироскопа относительно оси X. Окончательно получим.

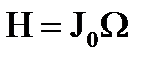(1.8)

Таким образом, собственный кинетический момент гироскопа равен произведению осевого момента инерции ротора гироскопа на его собственную угловую скорость.

Направление вектора кинетического момента Н совладает с направлением вектора угловой скорости .

Предположим, что в то время, когда гироскоп вращается вокруг своей главной оси X с угловой скоростью , эта ось не остается неподвижной, а изменяет направление в пространстве, вращаясь вокруг точки О. Как в этом случае определить кинетический момент гироскопа относительно неподвижной точки О?

Очевидно, что его значение не равно , а направление не совпадает с направлением оси X, поскольку суммарный вектор кинетического момента является результирующим двух составляющих векторов кинетических моментов. Однако, если гироскоп вращается вокруг оси X с большой угловой скоростью 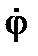между тем как ось X изменяет свое направление в пространстве сравнительно медленно, при вычислении кинетического момента можно пренебречь движением оси X. В этом случае значение кинетического момента H выражается формулой 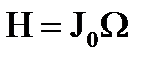, а направление вектора H совпадает с направлением оси X.

Кинетический момент Н гироскопа является наиболее полной характеристикой вращающегося тела, поскольку ни масса тела, ни его момент инерции, ни угловая скорость его вращения по отдельности не отражают его гироскопических свойств.

Дата добавления: 2015-10-21