Применение теоремы о кинетическом моменте для доказательства свойств гироскопа

Теорема о кинетическом моменте позволяет доказать основные свойства гироскопа.

Устойчивость главной оси свободного гироскопа. Для доказательства этого свойства необходимо в выражение (1.5) подставить значение , так как условие свободного гироскопа означает, что он свободен от действии каких-либо моментов внешних сил.

Следовательно, для свободного гироскопа , т. е. .

Иначе говоря, значение и направление кинетического момента гироскопа постоянны. Имея в виду, что 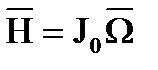(где осевой момент инерции гироскопа — величина постоянная), можно сделать вывод, что угловая скорость также постоянная.

Известно, что для быстровращающегося гироскопа направление кинетического момента совпадает с направлением оси X гироскопа, т. е. с направлением его главной оси. Следовательно, неизменность направления свидетельствует о неизменности направления в пространстве главной оси свободного гироскопа. Это подтверждает свойство устойчивости главной оси свободного гироскопа в пространстве.

Прецессия гироскопа. Рассмотрим гироскоп (рис. 1.6), на который действует сила 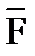, создающая момент 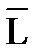вокруг какой-либо оси, не совпадающей с главной осью гироскопа (на рисунке вокруг оси Y). Как известно, кинетический момент быстровращающегося гироскопа следует считать направленным по главной оси. Конец вектора обозначим N.

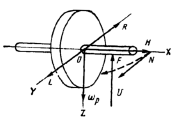Согласно теореме Резаля выражение означает, что конец вектора , т. е. точка N, приобретает линейную скорость, равную и параллельную вектору момента .

Рис. 1.5. К объяснению второго свойства гироскопа - прецессии

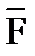На рис. 1.5 видно, что движение главной оси гироскопа происходит не в направлении действии приложенной силы , а в плоскости ХОУ перпендикулярно силе в направлении момента этой силы, т. е. мы наблюдаем случай прецессионного движения гироскопа. Оно возникает тогда, когда момент приложенных сил не совпадает по направлению с моментом .

Рассматривая рис. 1.5. сформулируем правило, пользуясь которым, можно на практике определять направление прецессии: прецессионное движение всегда совершается в том направлении, в котором вектор кинетического момента кратчайшим путем поворачивается к вектору момента приложенной силы. Угловая скорость прецессионного движения гироскопа численно равна линейной скорости , деленной на радиус вращении , т. е. на H: . Но по теореме Резаля , поэтому

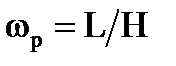(1.9)

Формула (1.9) выражает очень важный в прикладной теории гироскопов закон прецессии. Таким образом, угловая скорость прецессии прямо пропорциональна приложенному моменту внешних сил и обратно пропорциональна кинетическому моменту гироскопа.

Устойчивость к удару. Математическое выражение (1.5) теоремы о кинетическом моменте можно представить в конечных приращениях

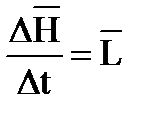
или

Рис. 1.5. К объяснению второго свойства гироскопа - удароустойчивости

(1.10)

Полученное выражение можно трактовать следующим образом: момент внешней силы , действующий на гироскоп в течение малого (в пределе бесконечно малого) времени , вызывает малое (в пределе бесконечно малое) изменение кинетического момента по направлению (рис. 1.6).

Угловое изменение . Если момент внешней силы действовал очень короткий интервал времени , то даже при большом значении момента величина , следовательно, мал угол . Отсюда вытекает важный практический вывод о том, чту импульс силы (удар) способен лишь незначительно изменить положение главной оси быстровращающегося гироскопа.

Дата добавления: 2015-10-21