Расчет раскосов

Все раскосы проектируем клееными одинакового сечения из 5 досок толщиной 26 мм. За расчетное усилие принимаем сжимающее усилие по табл. 2. Расчёт ведём для самого длинного раскоса 3-6.

Рис.5 Сечение раскоса

Исходя из предельной гибкости lmax=150 определяем минимальный размер сечения 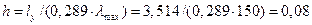Принимаем сечение раскосов .

Проверяем сечение раскоса на устойчивость по формуле:

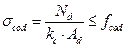
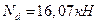- расчётное сжимающее усилие в раскосе 3-6

fc,0,d=14 МПа – расчетное сопротивление сосны сжатию для 2-го сорта для элементов прямоугольного сечения при высоте сечения до 0.5 м (табл. 6.5)

kх=1 –переходной коэфф. для сосны, учитывающий породу (табл. 6.6 [1]);

kmod=1,05 – коэффициент условий работы для учёта класса условий эксплуатации и класса длительности нагружения (табл. 6.4 [1]);

kh=1 – коэффициент, учитывающий высоту сечения, при h<0,5 м (табл. 6.7 [1]);

kd=1,05 – коэффициент, учитывающий толщину слоя, при d=26 мм (табл. 6.8 [1]);

kr=1 – коэффициент, учитывающий отношение радиуса кривизны к толщине доски, при r/b=1515/2,8=541>250 (табл. 6.9 [1]);

Запас прочности 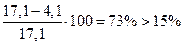, однако уменьшение сечения невозможно исходя из конструктивных условий и условия предельной гибкости.

3.3.3. Подбор сечения нижнего пояса

В соответствии с заданием принимаем пояс из равнополочных уголков.. Требуемая площадь сечения пояса A_тр=N´g_n/(R_y´g_c),

где: N=304,73 кН – максимальное усилие в панелях нижнего пояса (табл. 2);

R_y=240 МПа=24 кН/см² – расчетное сопротивление растяжению, сжатию и изгибу стали класса С245 толщиной от 2 до 20 мм (табл. 51*[5]);

g_c=0,95 – коэффициент условий работы при расчёте стальных конструкций (табл. 6* [5]).

A_тр=304,73´0,9/(24´0,95)=12,03 см². Из условия обеспечения гибкости панелей меньше предельной, принимаем 2 уголка 63х63х6 (ГОСТ 8509-93) общей площадью F=2*7,28=14,56 см² > 12,57 см².

Полки уголков соединяем сваркой через интервалы не более . Принимаем интервал 106,66см, т.е каждую панель длиной 533,3м разбиваем на 5 участков.

Проверим сечение второй панели нижнего пояса на совместное действие растягивающей силы и изгибающего момента в середине панели от собственного веса.

Геометрические характеристики сечения согласно ГОСТ 8509-93:

, ,

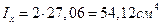Нагрузка от собственного веса уголка (масса 1 п.м уголка 5,72 кг согласно ГОСТ 8509-93): G_d=2*0,572=1,144 Н/см.

M=G_d´ 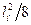=1,144´533,3²/8= 40,67 кН´см.

Напряжение в середине второй панели нижнего пояса:

s=3047,3/14,56+406,7/12,38=242,14МПа< R_y´g_c/g_n=240´0,95/0,9=253,3 МПа.

Запас прочности: 4,3%<15%.

Гибкость пояса в вертикальной плоскости:

l_х=l_н/i_х=533,3/1,93 =276 < l_max=400 (табл. 20* [5]).

Запас по гибкости 31%>15%. Несмотря на невыполнение условия гибкости, уменьшение сечения нижнего пояса невозможно по конструктивным соображениям.

3.3.4. Конструирование и расчет узлов

3.3.4.1. Опорный узел

В опорном узле верхний пояс упирается в плиту (упорная плита) с рёбрами жёсткости, приваренную к вертикальным фасонкам сварного башмака. Снизу фасонки приварены к опорной плите. Толщина фасонок принята 1,0 см.

Определяем площадь опирания торца верхнего пояса на упорную плиту башмака из условия смятия под действием сжимающей силы N_d=322,31 кН:

А_оп=N_d/f_cm,0,d=322,31/1,633=197,4 см²,

где f_cm,0,d=f_cm,0,d ´k_x´k_mod/g_n=14´1´1,05/0,9=16,33 МПа=1,633кН/cм²,

здесь f_cm,0,d = 14 МПа – расчетное сопротивление сосны смятию вдоль волокон для 2-го сорта для элементов прямоугольного сечения шириной от 0,11 до. 0,13 м при высоте сечения от 0,11 до 0,5 м (табл. 6.5 [1]).

Приняв ширину плиты равной ширине верхнего пояса находим длину плиты: l_п=А_оп/b_п=197,4/11,5=17,2 см. Конструктивно l_п=2´h/3=2´23,4/3=16 см.

Окончательно принимаем l_п=18 см.

Тогда: s_cm,0,d=322,31/(11,5´18)=1,56кН/cм² < f_cm,0,d=1,633 кН/cм².

Упорную плиту проектируем с рёбрами жёсткости.

Проверяем местную прочность на изгиб упорной плиты. Для этого рассмотрим среднюю часть упорной плиты как прямоугольную плиту, свободно опёртую по четырём сторонам, которыми являются вертикальные фасонки башмака и рёбра жёсткости упорной плиты.

Расчёт ведём по формулам теории упругости, приведенным в [6]. Расчётные пролёты опёртой по четырём сторонам плиты (рис. 2.5): a=9,4+1,0=10,4 см, b=12,6+1,0=13,6 см.

При b/a=13,6/10,4=1,31 согласно табл. 4.5 [6] a=0,0674.

Изгибающий момент в плите: M_п=a´s_cm,0,d´a²=0,0674´1,56´10,4²=11,37 кН×см.

Крайние участки упорной плиты рассмотрим как консоли.

Расчёт ведём для полосы шириной 1 см.

При с = 3,8 см – М_к = s_cm,0,d´с²/2=1,56´3,8 ²/2=11,26 кН×см.

По наибольшему из найденных для двух участков плиты изгибающих моментов определяем требуемую толщину плиты по формуле (4.13) [6]:

t_пл,у³ = 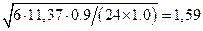см

где R_y=240 МПа=24,0 кН/см² – расчетное сопротивление при изгибе стали класса С245 толщиной от 2 до 20 мм (табл. 51* [5]).

Принимаем t_пл,у=16 мм.

Проверяем общую прочность упорной плиты на изгиб. Расчёт ведём приближенно как расчёт балок таврового сечения (рис. 5) пролётом, равным расстоянию между осями вертикальных фасонок l=12,6+1=13,6 см.

Нагрузка на рассматриваемую полосу плиты: N=O₁/2=322,31/2=161,2 кН,

где O₁=322,31 кН – максимальное сжимающее усилие в опорной панели верхнего пояса (табл. 2).

Интенсивность нагрузки под торцом элемента верхнего пояса шириной 14,0 см: q=161,2/11,5=14,0 кН/см.

Изгибающий момент в балке таврового сечения:

М =161,2´13,6/4–14´13,6²/8 = 224,4 кН×см.

По рис. 4 определяем момент сопротивления заштрихованной части сечения:

S_x=1,8´9´(4,0+1,7/2)+1,0´4,0´2,0=86,57 см³, А=1,0´4+1,8´9,0 = 20,2 см²,

y=S_x/А=86,57/20,2=4,29 см,

I_x=9´1,8³/12+9´1,8´0,61² + 1.0´4,0³/12+1,0´4,0´2,29²=36,71 см⁴,

W_min=I_x/y=36,71/4,29=8,56 см³.

s=224,4´10/8,56=262,2 МПа < R_y´g_c/g_n= 240´1,0/0,9 = 266, 7 МПа.

Запас прочности 1,4<15%

Рис. 6. Упорная плита башмака с рёбрами жёсткости

1 – опорная плита; 2 – вертикальные фасонки сварного башмака; 3 – упорная плита; 4 – рёбра жёсткости упорной плиты; 5 – болт ⌀14 мм, l=210 мм; 6 – верхний пояс фермы; 7 – нижний пояс фермы (2Ð63´63´6); 8 – соединительная прокладка l=115 мм.  

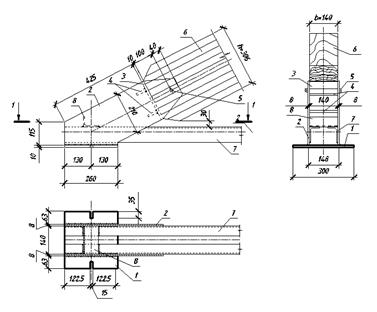
рис. 7. Опорный узел фермы

Рассчитываем опорную плиту (рис. 5). Полагаем, что опорная плита башмака опирается на брус из такой же древесины, что и ферма. Длину опорной плиты l_пл принимаем исходя из конструктивных требований (табл. 39 [5]) не менее значения:

l_пл,min=2´(b_уг+d_ф+2´1,5´d_от)+4=2´(6,3+1+2´1,5´1,3)=23,6 см, Принимаем 25cм.

где b_уг=6,3 см – ширина горизонтальной полки уголка нижнего пояса;

d_ф=1,0 см – толщина вертикальной фасонки;

d_от=1,3 см – предварительной принятый диаметр отверстия под болт, крепящий ферму к колонне.

Максимальная опорная реакция фермы:

F_А=0,5´G_d´l+0,229´Q_d,D´l=0,5´9,476´16+0,229´22,42´16=157,95 кН.

Требуемая ширина опорной плиты равна

b=F_А /(f_cm,90,d´l_п)=157,95/(0,35x25)=18,1см. Принимаем 19см

Напряжения смятия под опорной плитой:

s_cm,90,d=157,95/(19´25)=0,333МПа < f_cm,90,d´k_х´k_mod/g_n=3´1´0,95/0,9=0,35 МПа,

где f_cm,90,d=3 МПа – расчетное сопротивление сосны 2-го сорта местному смятию поперёк волокон в узловых примыканиях элементов (табл. 6.5 [1]).

Запас прочности 5%<15%.

Толщину опорной плиты (рис. 2.5) находим из условия изгиба:

— консольного участка М_к=s_cm,90,d´с²/2=0,333´5,2²/2=4,5 кН´см;

— среднего участка M_п=s_cm,90,d´a²/8=0,333´ 13,6²/8=7,7 кН´см,

где: с=5,2 см – вылет консоли;

а=13,6 см – пролёт среднего участка.

При ширине расчётной полосы в 1 см находим толщину плиту:

t_пл,оп³ = см.

Принимаем t_пл,оп=14 мм.

Находим длину сварных швов, крепящих уголки нижнего пояса к вертикальным фасонкам. Принимаем полуавтоматическую сварку в среде углекислого газа сварочной проволокой Св-08Г2С (ГОСТ 2246-70*), для которой R_wf=215 МПа (табл. 56 [5]). В соответствии с табл. 38* [5] принимаем по обушку катет шва k_f,о=6 мм, а по перу k_f,п=5 мм. Для выбранных катетов швов при полуавтоматической сварке b_f=0,9 и b_z=1,05 (табл. 34* [5]). Для стали класса С245 R_un=370 МПа (табл. 51* [5]) и соответственно R_wz=0,45´R_un=0,45´370=166,5 МПа.

Т.к. R_wz´b_z=166,5´1,05=174,8 МПа < R_wf´b_f=215´0,9=193,5 МПа расчёт ведём по металлу границы сплавления. Тогда, с учётом распределения усилия в первой панели нижнего пояса по перу и обушку (табл. 5.6 [6]), требуемые расчётные длины швов составят:

- по перу:

l_w,п=0,3´И₁´g_n/(R_wz´b_z´k_f,_п´g_с)=0,3´294,63´0,9´10/(166,5´1,05´0,5´0,95)=10,2 см;

- по обушку:

l_w,о=0,7´И₁´g_n/(R_wz´b_z´k_f,о´g_с) =0,7´294,63´0,9´10/(166,5´1,05´0,6´0,95)=18,1 см.

Принимаем l_w,п=11 см, l_w,о=19 см.

3.3.4.2. Коньковый узел

3.3.4.2.1. Расчёт крепления стальных пластинок-наконечников к раскосам

Принимаем пластинки-наконечники выполненными из полосовой стали толщиной 1,2 см и шириной 8,0 см. Число пластинок принимаем равное двум. Пластинку к раскосам крепим 4-мя болтами ⌀ 12 мм для исключения возможности возникновения эксцентриситета.

Расчётную несущую способность одного среза нагеля в двухсрезном соединении с обоими внешними элементами из стали согласно п. 9.4.1.14 [1] следует принимать равной меньшему значению из полученных по (9.13) и (9.14) [1]:

,

где f_h,1,d=8´k_х´k_mod=8´1´1,05=8,4МПа – расчётное сопротивление смятию древесины согласно табл. 9.1 и прим. табл. 9.2 [1];

t₂=11,5 см – ширина сечения раскоса;

d=1,2 см – диаметр нагеля;

=18´ =18´ =18,44 МПа – расчётное сопротивление изгибу нагеля согласно пп. 9.4.1.11 и 9.4.6.2 [1];

b_n,max=0,612 – коэффициент согласно п. 9.4.6.2 [1];

k_a=1 – коэффициент, учитывающий угол между силой и направлением волокон, при a=0° (табл. 9.3 [1]).

Тогда: R_ld,1=8,4´11,5´1,2´10^-1´1=9,27 кН,

R_ld,n=18,44´1,2²´(1+0,612²)´10^-1´ =3,64 кН.

Принимаем R_ld,min=3,64 кН и находим расчётное количество нагелей:

n_ef=N_d´g_n/(R_ld,min´n_s)=23,99´0,9/(3,64´2)=3,66 шт.,

где N_d=23,99 кН – максимальное расчётное усилие в раскосах (табл. 2);

n_s=2 – количество швов в соединении для одного нагеля.

Таким образом, принимаем количество болтов в соединении n_n=4 > n_ef =3,66, тогда расчётная несущая способность соединения будет равна:

R_d=R_ld,min´n_s´n_n/g_n=3,64´4´2/0,9=26,31 кН > N_d=23,99 кН.

Запас прочности составит: 8% < 15%

Проверим прочность на растяжение стальных пластинок-наконечников, ослабленных отверстиями под болты и гвозди: d_о,б=1,3 см,

N_max,+=Д₂=23,99 кН; А_n=2´1,2´(8–1,3–1,3)=12,96 см²;

s=N_max,+/А_n=23,99/12,96=1,85кН/см²=18,5 МПа < R_y´g_c/g_n=240´1,05/0,9=280 МПа.

Также проверим устойчивость стальных пластинок-наконечников из плоскости фермы между точками их закрепления узловым болтом и нагелями (рис. 7):

N_max,–=Д₃= -16,07 кН; l_p=45,5 см.

Гибкость пластин-наконечников: l=l_p/i=45,5/(0,289´1,2)=131,9.

s=N_max,– /(А´j)=16,07/(2´1,2´8´0,351)=2,38кН/см²=23,8 МПа <

R_y´g_c/g_n=240´0,95/0,9=253,0 МПа,

где j=0,351 – коэффициент продольного изгиба центрально-сжатых элементов при l=131,9 и R_y=240 МПа (табл. 72 [5])

Максимальная гибкость пластин-наконечников не превышает предельно допустимой:

l=131,9 < [l_max]=210–60´a=210–60´0,5=180 (табл. 19* [5]),

где a=s´g_n/(R_y´g_c)=23,8´0,9/240,0=0,08 < 0,5, поэтому a=0,5.

3.3.4.2.2 Конструирование сварного вкладыша и подбор диаметра узлового болта

В узлах верхнего пояса ставим сварные вкладыши, предназначенные для передачи усилий в блоках пояса и крепления раскосов (рис. 6). Площадь поверхностей плит вкладыша, соприкасающихся с торцами блоков верхнего пояса: А_п=b´h=11,5´18,0=207,0 см². Толщина плит вкладыша 1,2 см. Поскольку размеры поверхностей плит вкладыша такие же, как и упорной плиты в опорном узле, напряжения смятия не проверяем.

Проверяем прочность на изгиб плиты вкладыша с учётом постановки ребер жёсткости между плитами. Рассматриваем полосу плиты вкладыша шириной 1 см как двухпролётную балку с W=1´1,2²/6=0,24 см² и пролётом l= 3,95+1,2=5,15 см (см. рис. 6).

Максимальный изгибающий момент:

М_max=s_cm,0,d´l²/8=1,56 ´5,15²/8=5,17 кН´см.

Тогда: s=М_max/W=5,17/0,24=215 МПа<R_y´g_c/g_n=240´1,0/0,9=266,7 МПа.

Рассчитываем узловой болт, к которому крепятся раскосы, на изгиб от равнодействующей усилий в раскосах, которую определяем аналитически по теореме косинусов. Из табл. 2 выбираем при действии на ферму снеговой нагрузки, распределённой по треугольнику на половине пролёта: Д₂=23,99 кН, Д₃= -16,07 кН

рис. 6. Сварной вкладыш конькового узла

Тогда

N_r= =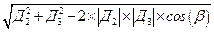

=

где b=90° – угол между раскосами Д₂ и Д₃.

Изгибающий момент в узловом болте: М_б=N_r´е/2 = 28,87´1,1/2=15,9 кН´см,

где е=0,8+0,3=1,1 см – эксцентриситет приложения усилия N_r (рис. 6).

В узлах верхнего пояса для восприятия монтажных усилий ставим симметричные деревянные накладки (рис. 6). Суммарная площадь поперечного сечения накладок должна быть не менее площади поперечного сечения верхнего пояса фермы.

Диаметр болта определяем по формуле:

d= = .

Принимаем узловой болт диаметром d=2,0 см.

1 – раскос; 2 – верхний пояс фермы; 3 – узловой болт ⌀20 мм, l=170 мм; 4 – накладки 100´180´640 мм; 5 – пластинки-наконечники 590´80´10 мм; 6 – болт ⌀12 мм, l=170 мм;

7 – болт ⌀12 мм, l=480 мм; 8 – подкладка 185´100´10 мм; 9 – сварной вкладыш;

10 – вырез в накладках; 11 – квадратная шайба 45´45´4 мм.

рис. 7. Коньковый узел фермы.

3.3.4.3. Нижний промежуточный узел

В узле нижнего пояса (рис. 8) уголки прерываются и перекрываются пластинами. В центре пластины просверлено отверстие для узлового болта. Исходя из условия размещения сварных швов, прикрепляющих уголки к пластинам, ширину последних назначаем 11,0 см.

Из условия прочности на растяжение стальной передаточной пластины, ослабленной отверстием под узловой болт, найдём её толщину:

d_о,б=1,5 см; N_max=И₂=304,73 кН (табл. 2); А_n=2´t_п.п.´(11,0–1,5)=19´t_п.п. см²;

А_n=N_max /(R_y´g_c/g_n) Þ t_п.п.=304,73´0,9´10/(19´240´1,05)=0,57 см.

Принимаем t_п.п=0,8 см.

Передаточные пластины соединяются с уголками нижнего пояса сварными швами такой же длины, как и в опорном узле.

Диаметр болта определяем из условия его изгиба от максимальной силы, выбранной из разности усилий в смежных панелях нижнего пояса и равнодействующей усилий в раскосах.

Максимальная разность усилий в смежных панелях нижнего пояса возникает при односторонней снеговой нагрузке, распределённой по треугольнику, и равна:

DИ=129,9+86,98–132,66-55,31=28,91 кН (см. табл. 2).

Равнодействующую усилий в раскосах определяем аналитически по теореме косинусов. Из таблицы 2 выбираем при действии на ферму снеговой нагрузки, распределённой по треугольнику на половине пролёта: Д₂=23,99 кН, Д₃= -20,76 кН.

Тогда N_r= = =31,9 кН,

где b=83° – угол между раскосами Д₃ и Д₂.

Изгибающий момент в узловом болте:

М_б=N_r´е/2=31,9´1,2/2=19,2 кН´см,

где е=0,8+0,4=1,2 см – эксцентриситет приложения усилия N_r (рис. 8).

Диаметр болта определяем по формуле:

d= = = =1,93 см.

Принимаем узловой болт диаметром d=2,0 см.

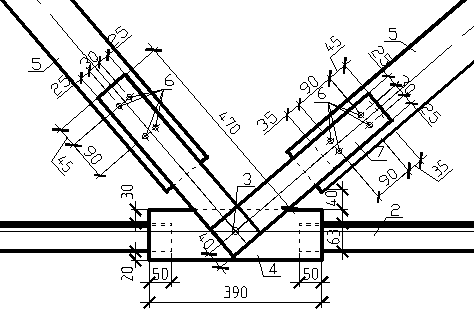
1 – раскос; 2 – нижний пояс фермы (2Ð63´63´6); 3 – узловой болт ⌀20 мм, l=170 мм; 4 – передаточная пластина 390´110´12 мм; 5 – пластинки-наконечники 470´80´12 мм; 6 – болт ⌀12 мм, l=170 мм; 7 – подкладка 160´800´12 мм;

рис. 8. Нижний промежуточный узел фермы

4. Статический расчёт поперечной рамы и подбор сечения колонны

4.1. Определение вертикальных нагрузок на раму

Расчетная постоян­ная нагрузка от покрытия, включая массу фермы (см. п. 3.2):

G_d=9,476кН/м².

Расчетное давление на колонну от покрытия: =G_d´l/2=9,476´16/2=75,8 кН,

То же от стенового ограждения с учетом элементов крепления;

=( + ´g_f)´В´Н=(0,785+0,1´1,05)´3,8´4=13,5 кН,

где =0,785 кН/м² – расчётная нагрузка от стенового ограждения, принятая равной расчётной нагрузки от покрытия (см. п. 3.2);

=0,10 кН/м² – масса металлических элементов крепления стенового ограждения;

g_f=1,05 – коэффициент надёжности по нагрузке для металлических конструкций (табл. 1 [2]);

Н=4,0 м – высота здания в свету.

Для определения собственной массы колонны ориентировочно при­нимаем следующие размеры ее сечения:

h=1/12´H=1/12´4,0=0,33 м, b=h/4=0,33/4»0,083 м.

Тогда расчетное давление от собственной массы колонны:

=b´h´H´r´g_f=0,33´0,083´4,0´500´10^-2´1,1=0,61кН,

где r=500 кг/м³ – плотность древесины сосны для 1 класса условий эксплуатации (табл. 6.2 [1]);

g_f=1,1 – коэффициент надежности по нагрузке (табл. 1 [2]).

Расчетное давление на колонну от снеговой нагрузки:

=0,229Q_d,s´B´l=0,229´22,42´16=82,15 кН,

где Q_d,s=22,42 кН/м² – расчетная снеговая нагрузка на 1 м² плана пок­рытия при равномерном распределении по всему пролету (см. п. 3.2).

4.2. Определение горизонтальных нагрузок на раму

Расчетная ветровая распределенная нагрузка на раму по высоте колонны определяется по формуле:

Q_d,w = w_m´g_f´B=w₀´k´c´g_f´B,

где g_f=1,4 – коэффициент надежности по ветровой нагрузке (п. 6.11 [2]).

Определяем расчетную распределенную нагрузку с наветренной сторона (напор):

— на высоте 4 м Q_d,w,1=0,6´0,4´0,8´1,4´3,8=1,02 кН/м,

где w₀=0,6 кПа=0,6 кН/м² –нормативное значение ветрового давления для V ветрового района (табл. 5 [2]);

k=0,4 – коэффициент для типа местности "С" соответственно при z £5 м (табл. 6 [2]);

с_е=0,8 – аэродинамический коэффициент с наветренной стороны (схема 3 прил. 4 [2]).

Определяем расчетную распределенную нагрузку с подветренной стороны (отсос):

— на высоте 4 м Q`_d,w,1=0,6´0,5´(-0,5)´1,4´3,8=-0,798 кН/м,

где с_е3 –0,5 – аэродинамический коэффициент с подветренной стороны при L/l=38/16=2,4>2 и Н/l=4,0/16=0,25<0,5 (схема 2 и 3 прил. 4 [2]).

Расчетную сосредоточенную ветровую нагрузку Q_d,w,3 на уровне нижнего пояса определим как сумму горизонтальных проекций результирующих нагрузок на участках l₁ и l₂, рис. 9.в.

Предварительно определим необходимые геометрические размеры.

Половина центрального угла j:

cos(j/2)=[(r–h_max)/r]=[(15,15–2,285)/ 15,15])=0,8492, j/2=31,88°.

Угол j₂:

cos(j₂)=[(r–0,3´h_max)/r]=[(15,15–0,3´2.285)/ 15,15)=0,9547, j₂=17,32°.

Угол j₁: j₁=j/2–j₂=31,88°–17,32°=14,56°,

где r=15,15м – радиус очертания оси верхнего пояса фермы (см. п. 3.1).

Длина дуги l₁=p´r´j₁/180°=3,14´15,15´14,56°/180°=3,85 м.

Длина дуги l₂=p´r´j₂/180°=3,14´15,15´17,32°/180°=4,58 м.

Угол a₁=90°–j₂–j₁/2=90°–17,32°–14,56°/2=65,4°,

Угол a₂=90°–j₂/2=90°–17,32°/2=81,34°.

Расчетная сосредоточенная нагрузка с наветренной стороны будет равна:

Q_d,w,3=w₀´k₁´c_е1´g_f´l₁´B´cos(a₁)+w₀´k₂´c_е2´g_f´l₂´B´cos(a₂)=

=0,6´0,4´(–0,1975)´1,4´3,85´3,8´0,4162+

0,6´0,4´(-0,84)´1,4´4,58´3,8´0,1506= – 1,144 кН,

где k₁=0,4 при z=Н+0,7´h_max/2=4,0+0,7´2,285/2=4,79 м (табл.6 [2]);

k₂=0,4приz=Н+0,7´h_max+0,3´h_max/2=4,0+0,7´3,86+0,3´2,285/2=4,34 (табл.6 [2]);

c_е1 –0,1975; c_е2 –0,84 – аэродинамические коэффициенты при h_max/l=2,285/16=0,1429 и Н/l=4,0/16=0,25 (схема 3 прил. 4 [2]);

cos(a₁)=0,4162, cos(a₂)=0,1506.

То же, с подветренной стороны:

Q`_d,w,3=w₀´k₁´c_е´g_f´l₁´B´cos(a₁)+w₀´k₂´c_е2´g_f´l₂´B´cos(a₂)=

=0,6´0,4´(–0,4)´1,4´3,85´3,8´0,4162+

0,6´0,4´(-0,84)´1,4´4,58´3,8´0,1506=-1,558кН,

где c_е –0,4 – аэродинамический коэффициент (схема 3 прил. 4 [2]).

4.3. Статический расчет рамы

Поскольку рама является один раз статически неопределимой системой, то определяем значение лишнего неизвестного, которым является продольное усилие в ригеле “F_Х”. Расчет выполняем для каждого вида загружения:

— от ветровой нагрузки на стены:

F_Х,w,1 –(Q_d,w,1+Q`_d,w,1)´р³´(4´Н–р)/(16´Н³) –(1,02–0,798)´5³´(4´4–5)/(16´4³)=

= –0,298 кН,

где H=4 м – высота загружения ветровой нагрузкой (рис. 9.б);

— от ветровой нагрузки, приложенной в уровне ригеля:

F_Х,w,3 –(Q_d,w,3+Q`_d,w,3)/2 –(–1,144–1,558)/2=1,35 кН;

— от стенового ограждения:

F_Х,ст –9´М_ст/(8´Н) –9´(–8,775)/(8´4,0)=2,47 кН,

где М_ст= ´е –13,5´0,65 –8,775 кН´м,

здесь е=0,5´(h_п+h)=0,5´(0,097+0,33)=0,65 м – расстояние между серединой колонны и стенового ограждения, толщина стенового ограждения принята равной высоте сечения деревянной составляющей покрытия.

Примем, что положительное значение неизвестного “F_Х” направлено от узлов рамы (на рис. 9.б показано сплошной линией), а изгибающeгo момента – по часовой стрелке. Определим изгибающие моменты в заделке рамы.

Для левой колонны:

М_d,л=[(Q_d,w,3+F_Х,w,1+F_Х,w,2+F_Х,w,3)´H+Q_d,w,1´p²/2]´y₂+F_Х,ст´H+М_ст =

=((–1,144–0,298+1,35)´4,0+1,02´5²/2) ´0,9+2,47´4-8,775=12,25 кН×м;

Для правой колонны:

М_d,пр=[(Q`<sub>d,w,3</sub>+F<sub>Х,w,1</sub>+F<sub>Х,w,2</sub>+F<sub>Х,w,3</sub>)´H+Q`_d,w,1´p²/2]´y₂+F_Х,ст´H+М_ст=

=((+1,558+0,298-1,35)´4,0+0,798´5²/2) ´0,9-2,47´4+8,77=9,69кН×м;

Поперечная сила в заделке:

V_d,л=[Q_d,w,3+F_Х,w,1+F_Х,w,2+F_Х,w,3+Q_d,w,1´p]´y₂+F_Х,ст=

=[–1,144-0,298+1,35+1,02´5]´0,9+2,47=6,97 кН;

V_d,пр=[Q`<sub>d,w,3</sub>+F<sub>Х,w,1</sub>+F<sub>Х,w,2</sub>+F<sub>Х,w,3</sub>+Q`_d,w,1´p]´y₂+F_Х,ст=

=[1,558+0,298-1,35+0,798´5]´0,9-2,47=1,58 кН;

Расчетные усилия:

М_d=М_d,л=12,25 кН´м; V_d=V_d,л=6,97 кН;

N_d= + + + ´y₂=75,8+13,5+0,61+82,15´0,9=163,5 кН,

где y₂=0,9 – коэффициент сочетания согласно п. 1.12 [2], учитывающий действие двух кратковременных нагрузок.

4.4. Подбор сечения колонны

Т.к. Н=8,0 м – отметка низа стропильных конструкций, то определим расчётную длину колонны по формуле:

Н_к=Н–h_об=4,0–0,075-0,15=3,775 м,

где h_об³В/(0,289´l_max)=380/(0,289´200)=6,6 см, принимаем h_об=7,5 см (п. 5.3.1.15, прил. Б, табл. Б.1 [1]) – высота сечения обвязочного бруса из условия устойчивости,

здесь В=3,8 м – шаг несущих конструкций;

l_max=200 – предельная гибкость для связей (табл. 7.2 [1]).

Проектируем колонну прямоугольного сечения, рис. 9. Ширину сечения определяем (b³100 мм) из условия предельной гибкости из плоскости рамы

b_тр=Н/(0,289´l_max)=(377,5)/(0,289´120)=10,88 см,

где Н_к – расчетная длина колонны;

l_max=120 – предельная гибкость колонны (табл. 7.2 [1]).

Принимаем ширину сечения колонны 125 мм, что с учетом острожки досок по кромкам составит b=115 мм.

После назначения ширины сечения колонны надо проверить длину опорной плиты фермы l_пл по формуле:

l_пл,min=b+2´(а_швел+1,5´d_от)=11,5+2´(3+1,5´1,5)=22 см,

где b=11,5 см – ширина сечения колонны;

а_уг=3,0 см – расстояние от края элемента крепления (швеллера) (см. рис. 71 [7]) до центра отверстия под болт (прил. VI, табл. 13 [6]);

d_от=1,5 см – предварительной принятый диаметр отверстия под болт, крепящий ферму к колонне.

Высоту сечения колонны принимаем из 9 досок толщиной 36 мм (после острожки). Тогда высота сечения h=36´9=324 мм.

Геометрические характеристики сечения:

A_d=11,5´32,4=372,6 см², W_d=11,5´32,4²/6=2012 см³,

Проверим сечение сжато-изогнутого элемента по формуле (7.31) [1].

Таким образом: l_d,z=m_0,z´l_z=2,2´377,5=830,5 см,

где m_0,z=2,2 – при одном защемлённом и втором свободном конце стержня (табл. 7.1 [1]).

I_х=0,289´32.4=9,36 см;

l_х=830,5/9,36=88,7< l_max=120 (табл. 7.2 [1]);

f_c,0,d=f_c,0,d´k_х´k_mod´k_h´k_d/g_n=14´1´1,2´1´0,98/0,9=19,6 МПа=1,96 кН/cм²,

где: f_c,0,d=14 МПа – расчетное сопротивление сосны сжатию для 2-го сорта для элементов прямоугольного сечения шириной от 11см до 13см при высоте от 13 до 50см (табл. 6.5 [1]);

k_х=1 – переходной коэффициент для сосны, учитывающий породу древесины (табл. 6.6 [1]);

k_mod=1,2 – коэффициент условий работы при учёте кратковременного действия ветровой нагрузки (табл. 6.4 [1]);

k_h=1 – коэффициент, учитывающий высоту сечения, при h=0,324 м < 0,5 м (табл. 6.7 [1]);

k_d=0,98 – коэффициент, учитывающий толщину слоя, при d=36 мм (табл. 6.8 [1]).

k_,c=3000/88,7 ² = 0,38

k_m,c=1–163,5/(0,38´1,96´372.6)=0.411

163,5´10/372.6+1225´10/(0,411´2012)=19,2<19.6, то есть принятое сечение удовлетворяет условиям прочности. Как видно из расчёта на прочность недонапряжение составляет 2%.

Проверим принятое сечение на устойчивость плоской формы деформирования по формуле (7.35) [1].

Расчётная длина колонн из плоскости изгиба:

l_d,y=377.5´1=377,5 см,

где m_0,у=1,0 – при шарнирном закреплении концов стержня из плоскости изгиба (табл. 7.1 [1]);

i_y= =3,32 см;

l_y=377.5/3,32=113,6 < l_max=120 (табл. 16 [3]);

k_c=3000/(113,6²)=0,232;

k_inst=140´11,5²´1.66/(377,5´32,4)=2,51.

k_m,c=1–163,5/(0,232´1,96´372.6)=0.35

где k_f=1,75–0,75´a=1,75–0,75´0.119=1.66 принято по табл. 7.4 [1] для трапециидальной формы эпюры моментов при свободной растянутой кромке для нижней половины колонны,

здесь a=1.46/12,25=0.119 при моменте в опорном сечении М_d,оп=12,25 кН×м и моменте по середине высоты колонны в той же стойке:

М_d,с=((–1,144–0,298+1,35)´2,0+1,02´3²/2) ´0,9+2,47´2-8,775=1,46кН×м;

Таким образом:

163,5/(0,232´1,96´372,6)+[1225/(1,96´0,35´2,51´2012)]²=0.98<1,

где: n=2 – показатель степени для элементов без закрепления растянутой зоны из плоскости деформирования.

Т.е. устойчивость плоской формы деформирования колонны обеспечена.

Проверим сечение колонны на действие скалывающих напряжений при изгибе по формуле (7.25) [1]:

t_v,0,d £ f_v,0,d,

где t_v,0,d=V_d´S_sup/(I_sup´b_d),

здесь V_d=V_d/k_m,c=6,97/0,35=19,91 кН – расчётная поперечная сила;

S_sup – статический момент брутто сдвигаемой части поперечного сечения колонны относительно нейтральной оси;

I_sup – момент инерции брутто поперечного сечения колонны относительно нейтральной оси;

b_d=b=11,5 см – расчётная ширина сечения колонны;

f_v,0,d=f_v,0,d´k_х´k_mod´k_d/g_n=1,5´1´1,2´0,98/0,9=1,96 МПа,

здесь: f_v,0,d=1,5 МПа – расчетное сопротивление сосны 2-го сорта скалыванию вдоль волокон при изгибе клееных элементов (табл. 6.5 [1]);

k_х=1 – переходной коэффициент для пихты, учитывающий породу древесины (табл. 6.6 [1]);

k_mod=1,2 – коэффициент условий работы при учёте кратковременного действия ветровой нагрузки (табл. 6.4 [1]);

k_d=0,98 – коэффициент, учитывающий толщину слоя, при d=36 мм (табл. 6.8 [1]).

Тогда с учётом того, что для прямоугольных элементов без ослаблений S_sup/I_sup=1,5/h, получаем:

t_v,0,d=19,91´1,5/(11,5´32,4)=0,08 кН/см²=0,8 МПа < f_v,0,d=1,96 МПа, т.е. условие выполнено.

4.5. Расчёт базы колонны

Жёсткое сопряжение колонны с фундаментом (рис. 11) осуществляем с помощью анкерных болтов. Анкерные болты прикрепляются к стальной траверсе, укладываемой на скошенные торцы специально приклеиваемых по бокам колонны бобышек.

Расчёт сопряжения производим по максимальному растягивающему усилию при действии постоянной нагрузки с коэффициентом надежности по нагрузке g_f=0,9 вместо среднего значения g_f,ср=1,1 и ветровой нагрузки (п. 2.2 [2]):

N_d=( + + )´g_f/g_f,ср=(75,8+13,6+0,61)´0,9/1,1=73,56 кН,

М_d=(Q`<sub>d,w,3</sub>+F<sub>Х,w,1</sub>+F<sub>Х,w,2</sub>+F<sub>Х,w,3</sub>)´H+Q`_d,w,1´p²/2+F_Х,ст´H´g_f/g_f,ср+М_ст´g_f/g_f,ср=

=(–1,144–0,298+1,35)´4,0+1,02´5²/2 +(2,47´4-8,775)´0,9/1,1=11,63 кН×м.

Определяем расчётный изгибающий момент с учётом его увеличения от действия продольной силы:

k_m,c=1–73,56/(0,35´372,6)=0,435;

М_d=М_d/k_m,c=11,63/0,435=26,66 кН×м.

Для крепления анкерных болтов по бокам колонны приклеиваем по две доски толщиной 36 мм каждая. Таким образом, высота сечения колонны у фундамента составляет h_н=468 мм. Тогда напряжения на поверхности фундамента будут составлять:

а) крепление колонны к фундаменту; 1–колонна; 2–бобышки; 3–косые шайбы; 4–анкерные болты ⌀20 мм; 5–болты ⌀12 мм; 6–траверса (Ð70´6); 7–гидроизоляция; 8–тяжёлый бетон класса С⁸/₁₀; б) эпюра напряжений на поверхности фундамента; в) расчётная схема траверсы; Рисунок 11. К расчёту базы колонны

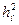s_max –N_d/(b´h_н)–6´М_d/(b´ )=–73,56/(11,5´32,4)–6´2666/(11,5´32,4²) –1,52 кН/см²;

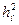s_min –N_d/(b´h_н)+6´М_d/(b´ )=–73,56/(11,5´32,4)+6´2666/(11,5´32,4²)=1,12 кН/см².

Для фундамента принимаем бетон класса С⁸/₁₀ с нормативным сопротивлением осевому сжатию f_ck=8,0 МПа (табл. 6.1 [8]). Расчётное сопротивление бетона на местное сжатие согласно п. 7.4.1.1 [8]:

f_cud=w_u´a´f_cd/g_n=1,2´0,85´5,33/0,9=6,04 МПа=0,604кН/см²,

где w_u – коэффициент, учитывающий повышение прочности бетона при смятии, который следует определять по формуле (7.146) [8], принимаем равным 1,2;

a=0,85 – коэффициент, учитывающий длительное действие нагрузки, принимаемый согласно указаниям п. 6.1.5.4 [8];

f_cd=f_ck/g_c=8/1,5=5,33 МПа – расчетное сопротивление бетона сжатию согласно указаниям п. 6.1.2.11 [8],

здесь g_c=1,5 – частный коэффициент безопасности по бетону.

Вычисляем размеры участков эпюры напряжений:

с_н=|s_max|´h_н/(|s_max|+|s_min|)=1,52´46,8/(1,52+1,12)=26,94 см;

а_н=h_н/2–с_н/3=46,8/2–26,94/3=14,42 см;

у=h_н–с_н/3–z=46,8–26,94/3–3,5=34,32 см,

где z=3,5 см – принятое расстояние от края колонны до оси анкерного болта (рис. 10.а).

Находим усилие в анкерных болтах:

N_б=(М_d–N_d´а_н)/у=(2666–73,56´14,42)/34,32=46,77 кН.

Требуемая площадь сечения анкерного болта:

А_тр=N_б´g_n/(n_б´R_ba)= 46.77´0,9/(2´18.5)=1,14 см²,

где n_б=2 – количество анкерных болтов с одной стороны;

R_ba=185 МПа=18,5 кН/см² – расчётное сопротивление растяжению анкерных болтов из стали марки ВСт3кп2 по ГОСТ 535-88

Принимаем болты диаметром 20 мм с расчётной площадью поперечного сечения А_bn=2,25 см² [ГОСТ 24379.0-80].

Траверсу для крепления анкерных болтов рассчитываем как балку по схеме, приведенной на рис. 10.в.

Изгибающий момент:

М=N_б´(l_т–b/2)/4=46,77´(14,5–11,5/2)/4=102,3 кН×см.

Из условия размещения анкерных болтов d=20 мм принимаем Ð70´6 с I_x=37,6 см⁴ и z₀=1.94 см (ГОСТ 8509-93) из стали класса С245.

Напряжения изгиба:

s=М´g_n´(b_уг–z₀)/I_x=102,3´0,9´(7,0–1.94)/37,6=12,4кН/см²=124МПа< R_y´g_c=240´1,1=264 МПа,

где: R_y=240 МПа – расчетное сопротивление изгибу стали класса С245 толщиной от 2 до 20 мм (табл. 51*[5]);

g_c=1,1 – коэффициент условий работы при расчёте стальных конструкций (табл. 6* [5]).

Проверяем прочность клеевого шва от действия усилия N_б согласно указаниям п. 9.3.5 [1]. Для этого определяем расчётную несущую способность клеевого шва на скалывание по формуле (9.3) [1]:

R_v,d=f_v,mod,d´A_v=0,29´575=166,8 кН,

где f_v,mod,d – расчётное среднее по площадке скалывания сопротивление древесины скалыванию вдоль волокон для клеевого шва, определяемое формуле (9.4) [1]:

f_v,mod,d=f_v,0,d/[1+b´(l_v/e)]=0,343/[1+0,125´(50/34.32)]=0,29 кН/см²,

здесьf_v,0,d=f_v,0,d´k_х´k_mod´k_d/g_n=2,1´1´1,2´0,98´0,125/0,9=3,43 МПа=0,343кН/см²

где: f_v,0,d=2,1 МПа – расчетное сопротивление сосны 2-го сортам местному скалыванию вдоль волокон в клеевых соединениях (табл. 6.5 [1]);

k_х=0,8 – переходной коэффициент для пихты, учитывающий породу древесины (табл. 6.6 [1]);

k_mod=1,2 – коэффициент условий работы при учёте кратковременного действия ветровой нагрузки (табл. 6.4 [1]);

k_d=0,98 – коэффициент, учитывающий толщину слоя, при d=36 мм (табл. 6.8 [1]).

b=0,125 – коэффициент при обеспечении обжатия площадки скалывания;

l_v=50 см – принятая длина клеевого соединения, т.е. расстояние от подошвы фундамента до стальной траверсы;

е=у=34,32 см – плечо сил скалывания;

A_v=b_v´l_v=11,5´50=575 см² – расчётная площадь скалывания,

здесь b_v=b=11.5 см – расчётная ширина участка скалывания.

Т.к. N_б=46,77 кН < R_v,d=166,8 кН, то прочность клеевого шва обеспечена.

5. Разработка схемы связей по шатру здания и колоннам

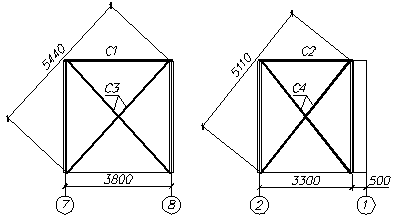
Рисунок 5.1 – Вертикальные связи по колоннам и их расчетные длины

Обвязочный брус С1 (рисунок 5.1).

Проектируем брус прямоугольного сечения. Ширину и высоту сечения определяем из условия предельной гибкости:

Принимаем ширину и высоту сечения обвязочного бруса 75 мм.

Обвязочный брус С2 по торцам здания (рисунок 5.1).

Проектируем брус прямоугольного сечения. Ширину и высоту сечения определяем из условия предельной гибкости:

Принимаем ширину и высоту сечения обвязочного бруса 75 мм.

Вертикальные связи по колоннам С3 (рисунок 5.1).

Исходя из предельной гибкости , определяем минимальный размер сечения вертикальной связи:

Принимаем сечение вертикальной связи b´h=100х100 мм,

Проверяем сечение связи по гибкости:

(п. 5.2.15 [1]);

; ;

;

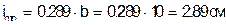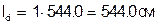Запас прочности по гибкости .

Вертикальные связи по колоннам С4 по торцам здания (рисунок 5.1).

Исходя из предельной гибкости , определяем минимальный размер сечения вертикальной связи:

Принимаем сечение вертикальной связи b´h=100х100 мм,

Проверяем сечение связи по гибкости:

(п. 5.2.15 [1]);

; ;

;

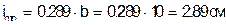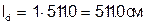Запас прочности по гибкости .

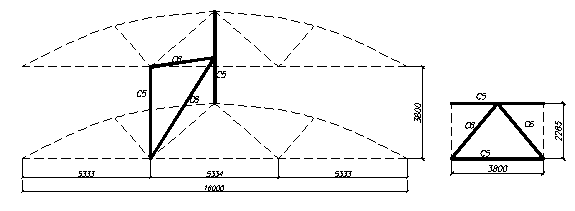
Рисунок 5.2 – Вертикальные (наклонные) связи по ферме и их расчетные длины

Распорка вертикальной связи по ферме С5 (рисунок 5.3).

Проектируем связи прямоугольного сечения. Ширину и высоту сечения определяем из условия предельной гибкости:

Принимаем ширину и высоту сечения связи 75 мм.

Вертикальная (наклонная) связь по ферме С6 (рисунок 5.2, 5.3).

Исходя из предельной гибкости , определяем минимальный размер сечения вертикальной связи:

Принимаем сечение вертикальной связи b´h=75х75 мм,

Проверяем сечение связи по гибкости:

(п. 5.2.15 [1]);

; ;

;

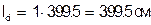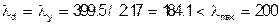Запас прочности по гибкости .

Распорка вертикальной связи по ферме С7 по торцам здания (рисунок 5.5).

Проектируем связи прямоугольного сечения. Ширину и высоту сечения определяем из условия предельной гибкости:

Принимаем ширину и высоту сечения связи 75 мм.

Вертикальная (наклонная) связь по ферме С8 по торцам здания (рисунок 5.4, 5.5)

Исходя из предельной гибкости , определяем минимальный размер сечения вертикальной связи:

Принимаем сечение вертикальной связи b´h=75х75 мм,

Проверяем сечение связи по гибкости:

(п. 5.2.15 [1]);

; ;

;

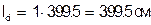Запас прочности по гибкости .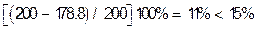

Рисунок 5.3 – Скатные связи по ферме и их расчетные длины

Распорка скатной связи по ферме С9 (С5) (рисунок 5.3).

Проектируем связи прямоугольного сечения. Ширину и высоту сечения определяем из условия предельной гибкости:

Принимаем ширину и высоту сечения связи 75 мм.

Раскос скатной связи по ферме С10 (рисунок 5.6).

Исходя из предельной гибкости , определяем минимальный размер сечения вертикальной связи:

Принимаем сечение вертикальной связи b´h=75х75 мм,

Проверяем сечение связи по гибкости:

(п. 5.2.15 [1]);

; ;

;

Запас прочности по гибкости .

Рисунок 5.4 – Скатные связи по ферме и их расчетные длины в торцевых пролётах

Распорка скатной связи по ферме С11 (С7) по торцам здания (рисунок 5.3).

Проектируем связи прямоугольного сечения. Ширину и высоту сечения определяем из условия предельной гибкости:

Принимаем ширину и высоту сечения связи 75 мм.

Раскос скатной связи по ферме С12 по торцам здания (рисунок 5.3).

Исходя из предельной гибкости , определяем минимальный размер сечения вертикальной связи:

Принимаем сечение вертикальной связи b´h=75х75 мм,

Проверяем сечение связи по гибкости:

(п. 5.2.15 [1]);

; ;

;

Запас прочности по гибкости .

Литература

1. Деревянные конструкции. Строительные нормы проектирования: ТКП 45-5.05- 146-2009 (02250). - Введ. 01.01.2010. - Мн.: Министерство архитектуры и строительства Республики Беларусь. 2009. - 63 с. Технический кодекс устано­вившейся практики.

2. Строительные нормы и правила. Нагрузки и воздействия: СНиП 2.01.07-85. - Введ. 01.01.1987. - М.: Госстрой СССР, 1987. - 36 с., с изменением №1.

3. Строительные нормы и правила. Нагрузки и воздействия: СНиП 2.01.07-85 (Дополнения. Раздел 10. Прогибы и перемещения). - Введ. 01.01.1989. - М.: ЦНИТП Госстроя СССР, 1989. - 8 с.

4. Жук, В.В. Методическое пособие по курсовому проектированию по дис­циплине «Конструкции из дерева и пластмасс» для студентов специальности 1-70 02 01 «Промышленное и гражданское строительство» дневной и заочной форм обучения: учеб.-метод. пособие / В.В. Жук, И.Ф. Захаркевич, В.И. Игнатюк, Н.В. Черноиван. - Брест: УО БрГТУ, 2012. - 39 с.

5. Гринь, И.М. Строительные конструкции из дерева и синтетических материалов. Проектирование и расчет: учеб. пособие для строительных вузов и ф-тов / И.М. Гринь. - 2-е изд., перераб. и доп. - Киев-Донецк: Вища школа, головное изд-во, 1979. - 272 с.

6. Строительные нормы и правила. Стальные конструкции / Госстрой СССР — Введ. 01.01.1982.-М.: ЦИТП Госстроя СССР, 1988. - 96 с.

7. Расчёт стальных конструкций: справ. пособие / Я.М. Лихтарников, Д.В. Ладыжен­ский, В.М. Клыков. - 2-е изд, перераб. и доп. - К.: Будiвельник, 1984. — 368 с.

8. Жук, В.В. Справочные материалы для проектирования деревянных конструк­ций зданий и сооружений / В.В. Жук. — Брест: БрГТУ, 2010. — 33с.

9. Национальный комплекс нормативно-технических документов в строительстве. Строительные нормы Республики Беларусь. Бетонные и железобетонные конст­рукции: СНБ 5.03.01 - 02. - Введ. 01.07.2003. - Мн.: Министерство архитектуры и строительства Республики Беларусь. 2003. - 139 с., с изменениями №1 - №3.

10. Васильев А.А. Металлические конструкции: учеб. пособие для техникумов / А.А. Васильев - 2-е изд., перераб. и доп. - М.: Стройиздат, 1976. - 424 с.

11. Шурин, А.Б. Справочные материалы для проектирования стальных конструкций зданий и сооружений / А.Б. Шурин, А.В. Мухин. - Брест: БрГТУ, 2004. - 83 с.

12. Защита строительных конструкции от коррозии. Строительные нормы проек­тирования: ТКП 45-2.01-111-2008 (02250). - Мн.: Министерство архитектуры и строительства Республики Беларусь 2009. Технический кодекс установив­шейся практики. - 63 с.

13. Стандарт университета. Оформление материалов курсовых и дипломных про­ектов (работ), отчётов по практике. Общие требования и правила оформления: СГ БГТУ 01-2008. - Брест: БрГТУ, 2008. - 46 с.

Дата добавления: 2015-10-21